声明

本博客只是记录一下本人在深度学习过程中的学习笔记和编程经验，大部分代码是参考了【中文】【吴恩达课后编程作业】Course 2 - 改善深层神经网络 - 第一周作业(1&2&3)这篇博客，对其代码实现了复现，代码或文字表述中还存在一些问题，请见谅，之前的博客也是主要参考这个大佬。

一、任务描述

这次作业我们的主要任务是以下三个：

1.初始化参数：0初始化，随机初始化，使用抑梯度异常初始化参数。
2.正则化：L2正则化，dropout正则化。
3.梯度校验  ：对模型使用梯度校验，检测它是否在梯度下降的过程中出现误差过大的情况。

本次作业的重点是在参数初始化，正则化和梯度检验上，因此对于神经网络的相关实现进行过多描述。三个知识点对于神经网络的要求并不完全相同，在正向和反向传播上存在差异，分别创建对应的 ==init_utils.py== ，==reg_utils.py== 和 ==gc_utils.py== 文件，封装神经网络的相关操作，神经网络统一为两层结构，即一个输入层，一个隐藏层和一个输出层。

二、编程实现

1.数据

本次作业提供了一份数据，用matplotlib绘制：

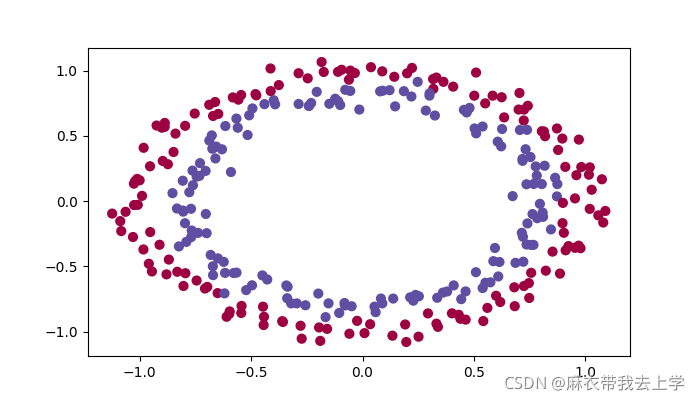
本次作业中要处理的问题也是一个二分类问题。

2.参数初始化

根据课程知识，我们可以分别对三种初始化的情形编程。

2.1 初始化参数为0

def initialize_zeros(layers_dims):
    """
    将参数都设置成0
    :param layers_dims:列表，各层的神经元个数
    :return:
    """
    parameters = {}
    for i in range(1, len(layers_dims)):
        parameters["W" + str(i)] = np.zeros((layers_dims[i], layers_dims[i - 1]))
        parameters["b" + str(i)] = np.zeros((layers_dims[i], 1))

        assert(parameters["W" + str(i)].shape == (layers_dims[i], layers_dims[i - 1]))
        assert (parameters["b" + str(i)].shape == (layers_dims[i], 1))
    return parameters

2.2 参数随机初始化

def initialize_random(layers_dims):
    """
    将W随机初始化,b依旧初始化为0
    :param layers_dims:列表，各层的神经元个数
    :return:
    """
    np.random.seed(3)
    parameters = {}
    for i in range(1, len(layers_dims)):
        parameters["W" + str(i)] = np.random.randn(layers_dims[i], layers_dims[i - 1])*10
        parameters["b" + str(i)] = np.zeros((layers_dims[i], 1))

        assert (parameters["W" + str(i)].shape == (layers_dims[i], layers_dims[i - 1]))
        assert (parameters["b" + str(i)].shape == (layers_dims[i], 1))
    return parameters

2.3 抑梯度异常初始化

抑梯度异常初始化需要在随机初始化W矩阵的基础上乘上系数(1/n[L-1])^(1/2)，即上层神经元个数（也就是当前神经元的输入个数）的倒数取平方根。

def initialize_random_he(layers_dims):
    """
    将W随机初始化,b依旧初始化为0
    :param layers_dims:列表，各层的神经元个数
    :return:
    """
    np.random.seed(3)
    parameters = {}
    for i in range(1, len(layers_dims)):
        parameters["W" + str(i)] = np.random.randn(layers_dims[i], layers_dims[i - 1])*np.sqrt(2 / layers_dims[i - 1])
        parameters["b" + str(i)] = np.zeros((layers_dims[i], 1))

        assert (parameters["W" + str(i)].shape == (layers_dims[i], layers_dims[i - 1]))
        assert (parameters["b" + str(i)].shape == (layers_dims[i], 1))
    return parameters

2.4 主控函数

def model(X, Y, learning_rate=0.01, num_iterations=15000, print_cost=True, initialization="he", is_plot=True):
    """
    实现一个三层（双层隐藏层一层输出层）神经网络：RELU,RELU,SIGMOID
    :param X: 输入数据
    :param Y: 输入数据标签
    :param learning_rate:学习率
    :param num_iterations: 迭代次数
    :param print_cost: 是否打印损失值
    :param initialization: 参数初始化类型
    :param is_plot: 是否绘制梯度下降曲线
    :return:
    """
    grads = {}
    costs = []
    layers_dim = [X.shape[0], 10, 5, 1]
    sample_num = X.shape[1]

    # 随机初始化神经网络参数
    if initialization == "zeros":
        parameters = initialize_zeros(layers_dim)
    elif initialization == "random":
        parameters = initialize_random(layers_dim)
    elif initialization == "random_he":
        parameters = initialize_random_he(layers_dim)
    else:
        print("传参错误")

    for i in range(0, num_iterations):
        a3, cache = init_utils.forward_propagation(X, parameters)

        cost = init_utils.compute_loss(a3, Y)

        grads = init_utils.backward_propagation(X, Y, cache)

        parameters = init_utils.update_parameters(parameters, grads, learning_rate)

        if i % 1000 == 0:
            costs.append(cost)
            if print_cost:
                print("第" + str(i) + "次迭代，成本值为：" + str(cost))

    if is_plot:
        plt.plot(costs)
        plt.ylabel('cost')
        plt.xlabel('iterations (per hundreds)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()
    return parameters

2.5 测试结果对比

2.5.1 初始化为0

初始化参数为0时的损失函数曲线：

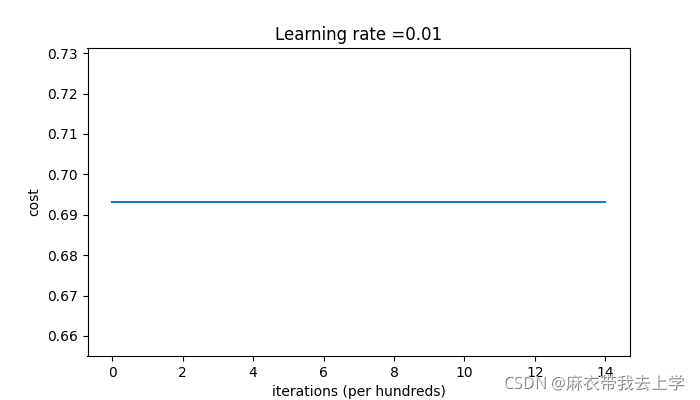
用matplotlib绘制初始化参数为0时的决策边界：

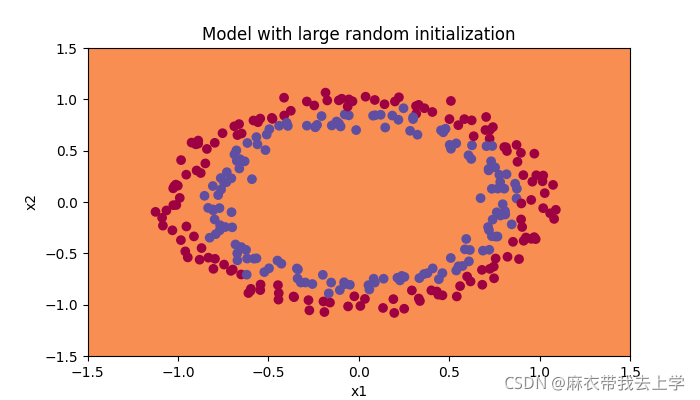
得到的模型在训练集和测试集上的表现效果：

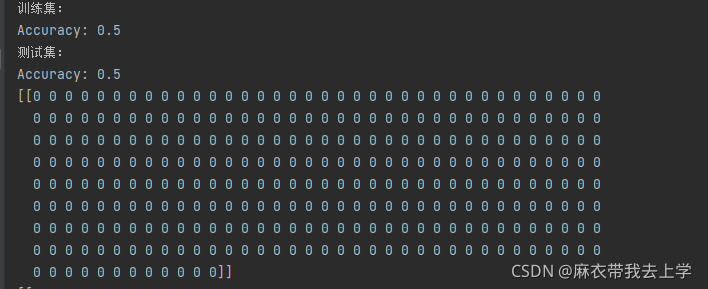
可以看出，初始化参数为0时，模型的表现效果非常差，预测的每个结果都为0。用0初始化神经网络参数无法打破网络的对称性。

2.5.2 随机初始化参数

绘制随机初始化损失曲线如下：

用matplotlib绘制决策边界：

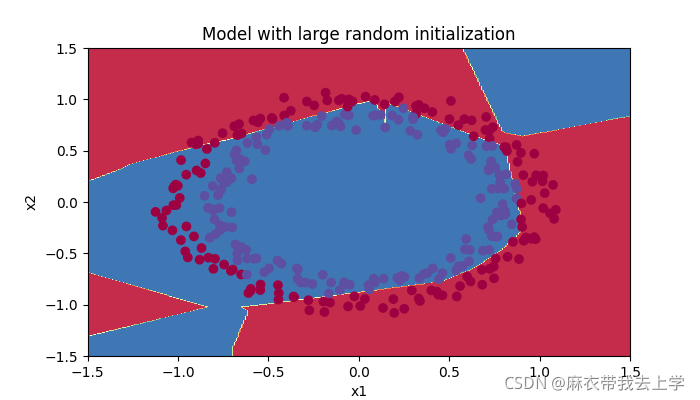
得到的模型在训练集和测试集上的表现效果：

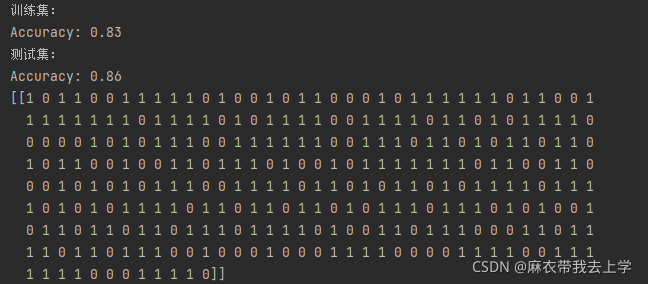
从结果可以看出，随机初始化的效果比初始化为0的效果好的多，但是随机初始化存在一些问题，上次作业中我提到过，如果权重矩阵随机初始化为较大的值会导致梯度消失和梯度爆炸，之前的解决方案是直接在初始化权重矩阵时乘上系数0.01，这里将尝试采用抑梯度异常初始化的方式来对权重矩阵的初始化进行控制。

2.5.3抑梯度异常初始化

绘制损失曲线如下：

用matplotlib绘制决策边界：

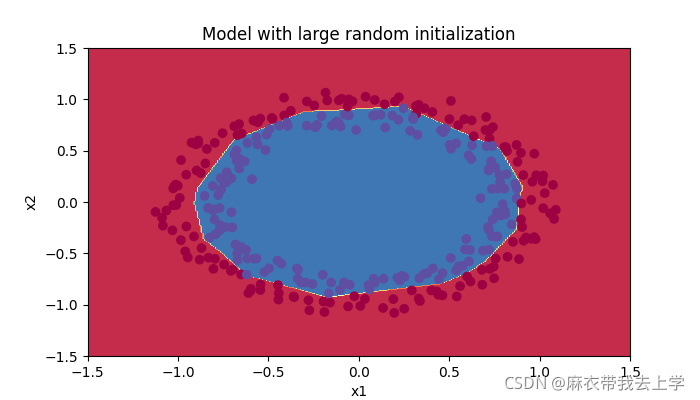
得到的模型在训练集和测试集上的表现效果：

从结果可以看出，抑梯度异常初始化的方法得到的模型表现效果特别好。

3.模型正则化

吴恩达老师的视频中主要讲述了两种正则化的方法：L2正则化和dropout正则化。这次我们需要使用到的数据分布如下：

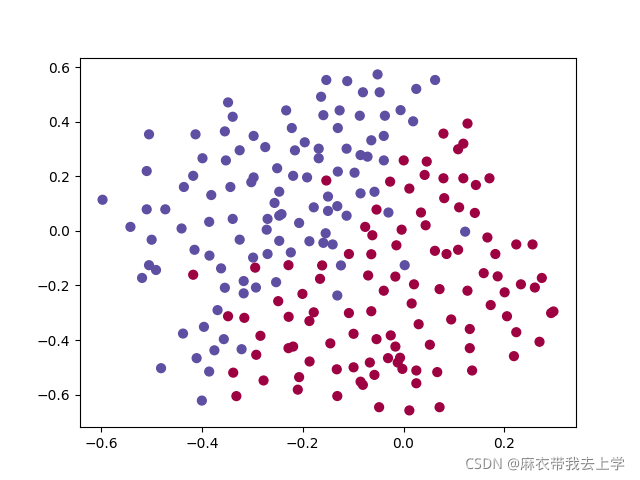
我们还是以两层神经网络为基础编写代码，主控函数代码如下：

def model(X, Y, learning_rate=0.3, num_iterations=30000, print_cost=True, is_plot=True, lambd=0, keep_drop=1):
    """
    三层神经网络(两层隐藏层):RELU,RELU,SIGMOID
    :param X: 输入数据
    :param Y: 标签值
    :param learning_rate:学习率
    :param num_iterations: 迭代次数
    :param print_cost: 是否打印损失值
    :param is_plot: 是否绘制损失曲线
    :param lambd: 正则化参数
    :param keep_drop: dropout参数
    :return:
    """
    grads = {}
    costs = []
    num_sample = X.shape[1]
    layers_dims = [X.shape[0], 20, 3, 1]

    parameters = reg_utils.initialize_parameters(layers_dims)

    for i in range(0, num_iterations):
        # 前向传播
        if keep_drop == 1:
            a3, cache = reg_utils.forward_propagation(X, parameters)
        elif keep_drop < 1:
            a3, cache = reg_utils.forward_propagation_with_dropout(X, parameters, keep_prob=keep_drop)

        # 计算损失
        if lambd == 0:
            cost = reg_utils.compute_cost(a3, Y)
        else:
            cost = reg_utils.compute_cost_with_regularization(a3, Y, parameters, lambd)

        # 反向传播
        if lambd == 0 and keep_drop == 1:
            grads = reg_utils.backward_propagation(X, Y, cache)
        elif lambd != 0:
            grads = reg_utils.backward_propagation_with_regularization(X, Y, cache, lambd)
        elif keep_drop < 1:
            grads = reg_utils.backward_propagation_with_dropout(X, Y, cache, keep_drop)

        # 更新参数
        parameters = reg_utils.update_parameters(parameters, grads, learning_rate)

        if i % 1000 == 0:
            ## 记录成本
            costs.append(cost)
            if print_cost and i % 1000 == 0:
                # 打印成本
                print("第" + str(i) + "次迭代，成本值为：" + str(cost))

    if is_plot:
        plt.plot(costs)
        plt.ylabel('cost')
        plt.xlabel('iterations (x1,000)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()

            # 返回学习后的参数
        return parameters

主控函数model需要传入参数 ==lambd== 和 ==keep_drop== 分别是L2正则化和dropout正则化需要的超参数。当lambd>0时，L2正则化才起作用。当keep_drop<1时，dropout正则化才起作用。接下来分别对这两种正则化方法进行编程。

3.1 未使用正则化

当我们往model中传入的参数lambd=0,keep_drop=1时表示不使用正则化。

if __name__ == "__main__":
    train_X, train_Y, test_X, test_Y = reg_utils.load_2D_dataset(is_plot=True)
    parameters = model(train_X, train_Y, is_plot=True)
    print("训练集:")
    predictions_train = reg_utils.predict(train_X, train_Y, parameters)
    print("测试集:")
    predictions_test = reg_utils.predict(test_X, test_Y, parameters)
    plt.title("Model without regularization")
    axes = plt.gca()
    axes.set_xlim([-0.75, 0.40])
    axes.set_ylim([-0.75, 0.65])

绘制损失曲线如下：

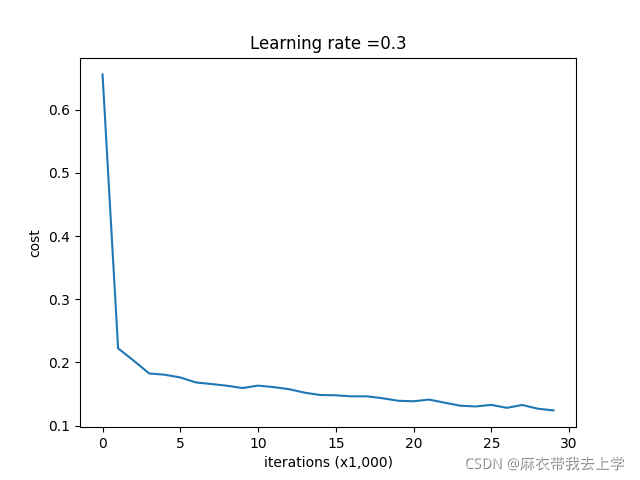
绘制决策边界：

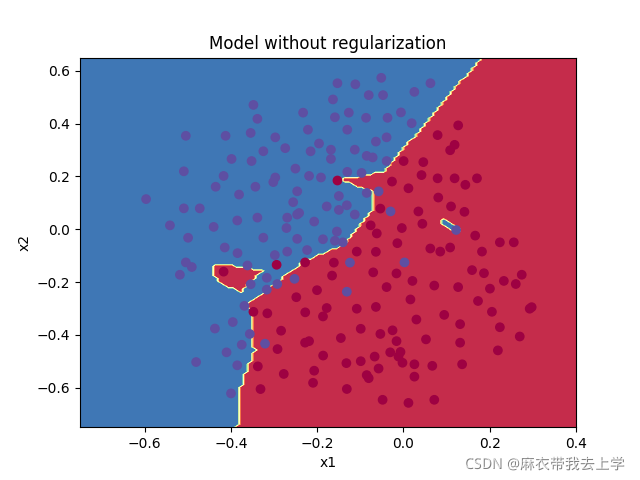
模型在训练集和测试集上的表现：

可以看到训练集上的准确率高于测试集上的准确率，可以视为过拟合现象，接下来通过L2正则化降低过拟合现象。

3.2 L2正则化

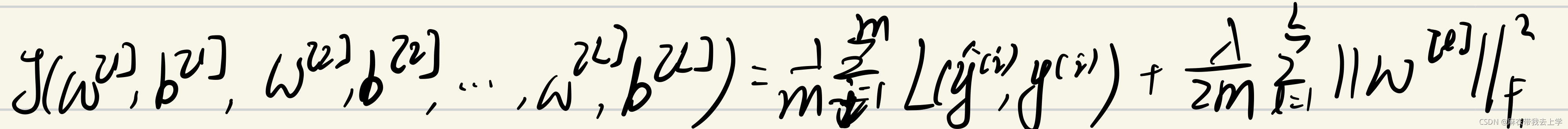
L2正则化是在损失函数的基础上加了正则项，这样其实并不会影响神经网络的正向传播，只需要对神经网络的反向传播代码和损失函数计算代码进行调整。

def backward_propagation_with_regularization(X, Y, cache, lambd):
    """
    实现正则化后的反向传播
    :param X: 输入数据
    :param Y: 实际标签值
    :param cache: forward的cache
    :param lambd: 正则化参数
    :return:
    """
    m = X.shape[1]
    (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache

    dZ3 = A3 - Y

    dW3 = (1 / m) * np.dot(dZ3, A2.T) + ((lambd * W3) / m)
    db3 = (1 / m) * np.sum(dZ3, axis=1, keepdims=True)

    dA2 = np.dot(W3.T, dZ3)
    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    dW2 = (1 / m) * np.dot(dZ2, A1.T) + ((lambd / W2) / m)
    db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)

    dA1 = np.dot(W2.T, dZ2)
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    dW1 = (1 / m) * np.dot(dZ1, X.T) + ((lambd * W1) / m)
    db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)

    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
                 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
                 "dZ1": dZ1, "dW1": dW1, "db1": db1}

    return gradients

损失函数计算代码：

def compute_cost_with_regularization(A3, Y, parameters, lambd):
    """
    实现L2正则化的损失函数计算
    :param A3: 输出层的输出值
    :param Y: 实际标签值
    :param parameters:神经网络参数
    :param lambd: 正则化参数
    :return:
    """
    cost_part1 = compute_cost(A3, Y)

    m = Y.shape[1]
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    W3 = parameters["W3"]

    L2_regularization_cost = lambd * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3))) / (2 * m)

    cost = cost_part1 + L2_regularization_cost
    return cost

设置超参数lambd=0.7,损失曲线绘制如下：

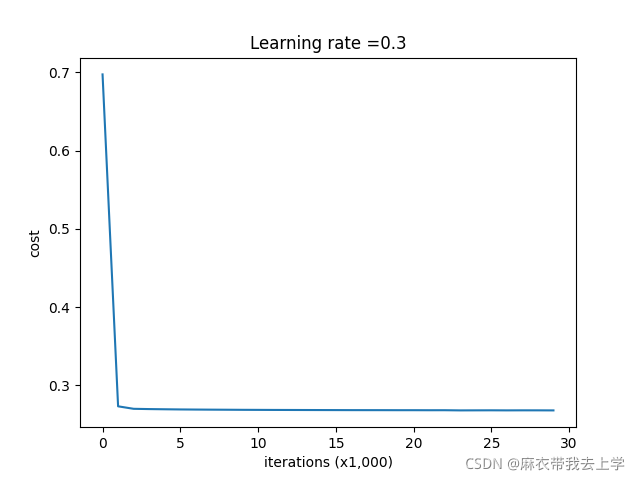
决策边界绘制如下：

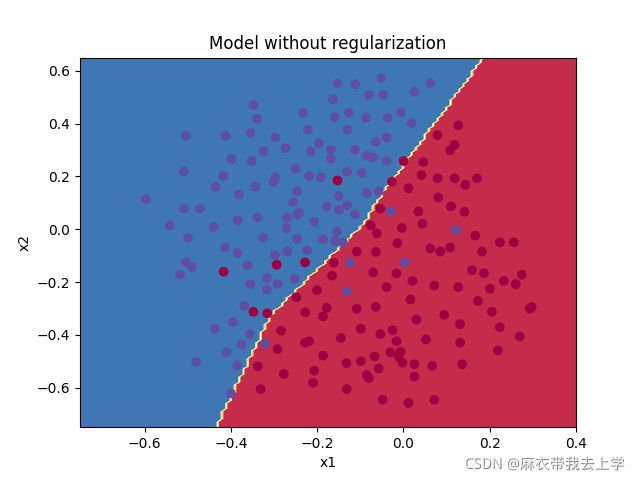
模型在训练集和测试集上的表现：

从结果可以看出，使用L2正则化的后，模型在训练集和测试集上的表现效果十分接近，有效的解决了过拟合。

3.3 dropout正则化

dropout正则化会影响常规的正向传播和反向传播，损失函数的计算没有影响。正向传播代码如下：

 """
    dropout正则化前向传播：RELU+DROPOUT,RELU+DROPOUT,SIGMOID
    :param X:输入数据
    :param parameters:神经网络参数
    :param keep_prob: dropout参数
    :return:
    """
    np.random.seed(1)
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]

    Z1 = np.dot(W1, X) + b1
    A1 = relu(Z1)

    D1 = np.random.rand(A1.shape[0], A1.shape[1])
    D1 = D1 < keep_prob
    A1 = A1 * D1
    A1 = A1 / keep_prob

    Z2 = np.dot(W2, A1) + b2
    A2 = relu(Z2)

    D2 = np.random.rand(A2.shape[0], A2.shape[1])
    D2 = D2 < keep_prob
    A2 = A2 * D2
    A2 = A2 / keep_prob

    Z3 = np.dot(W3, A2) + b3
    A3 = sigmoid(Z3)

    cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
    return A3, cache

反向传播代码如下：

def backward_propagation_with_dropout(X, Y, cache, keep_prob):
    """
    实现dropout正则化后的反向传播
    :param X: 输入数据
    :param Y: 标签值
    :param cache: 正向传播的缓存
    :param keep_prob: dropout正则化参数
    :return:
    """
    m = X.shape[1]
    (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache

    dZ3 = A3 - Y
    dW3 = (1 / m) * np.dot(dZ3, A2.T)
    db3 = (1 / m) * np.sum(dZ3, axis=1, keepdims=True)

    dA2 = np.dot(W3.T, dZ3)
    dA2 = dA2 * D2
    dA2 = dA2 / keep_prob

    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    dW2 = (1. / m) * np.dot(dZ2, A1.T)
    db2 = (1. / m) * np.sum(dZ2, axis=1, keepdims=True)

    dA1 = np.dot(W2.T, dZ2)
    dA1 = dA1 * D1
    dA1 = dA1 / keep_prob

    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    dW1 = (1. / m) * np.dot(dZ1, X.T)
    db1 = (1. / m) * np.sum(dZ1, axis=1, keepdims=True)

    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
                 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
                 "dZ1": dZ1, "dW1": dW1, "db1": db1}

    return gradients

将主控函数中的keep_drop的值设为0.86，绘制损失曲线如下：

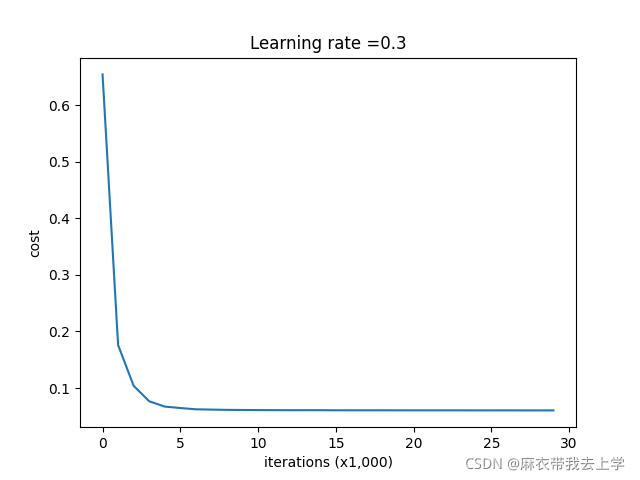
绘制决策边界：

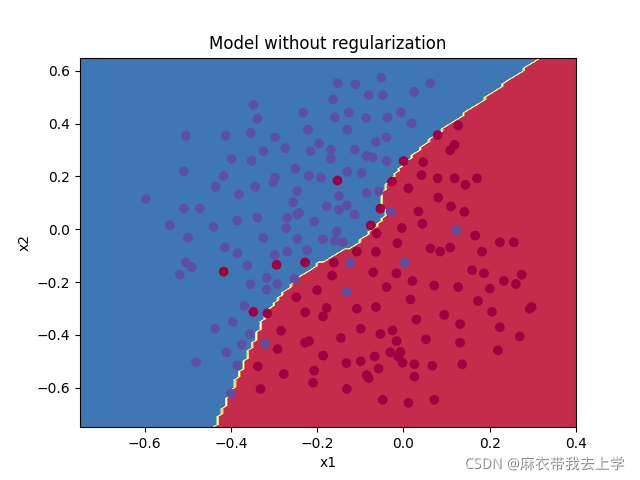
模型在训练集和测试集上的表现效果：

dropout正则化降低了模型在训练集上的准确率，提高了模型在测试集上的准确率，成功地解决了过拟合现象。另外，在写代码的过程中，初始化矩阵D时，使用了randn函数而不是rand函数，导致结果偏低。
rand和randn都是numpy库中生成的随机数的函数，但是rand是生成一个数组，并在数组中加入在[0,1]之间均匀分布的随机样本。randn则是创建一个数组，数组中的元素符合正态分布。很明显在dropout正则化中，我们需要初始化数组D中的数据在[0,1]之间均与分布，这样就可以保证D中小于keep_drop的元素占比为keep_drop。

总结

再次声明，本博客的主要代码参考来源为【中文】【吴恩达课后编程作业】Course 2 - 改善深层神经网络 - 第一周作业(1&2&3) - 初始化、正则化、梯度校验，原博客讲述更加详细。本人的代码已上传到百度网盘中，提取码：uu35。

声明

一、任务描述

二、编程实现

1.数据

2.参数初始化

2.1 初始化参数为0

2.2 参数随机初始化

2.3 抑梯度异常初始化

2.4 主控函数

2.5 测试结果对比

2.5.1 初始化为0

2.5.2 随机初始化参数

2.5.3抑梯度异常初始化

3.模型正则化

3.1 未使用正则化

3.2 L2正则化

3.3 dropout正则化

总结

发送评论 编辑评论

推荐文章

发送评论编辑评论