声明
本博客只是记录一下本人在深度学习过程中的学习笔记和编程经验,大部分代码是参考了【中文】【吴恩达课后编程作业】Course 2 - 改善深层神经网络 - 第一周作业(1&2&3)这篇博客,对其代码实现了复现,代码或文字表述中还存在一些问题,请见谅,之前的博客也是主要参考这个大佬。
一、任务描述
本次作业的目的是想让大家了解如何去搭建一个深层的神经网络,在第一周的作业中,我们利用了逻辑回归模型来识别猫的图片,该任务的本质就是搭建一个隐藏层数量为0(只有输入层和输出层)的神经网络来完成一个二分类任务。此次作业的任务其实有两个:
1.搭建一个隐藏层数量为1的神经网络;
2.搭建一个深层神经网络。我为了方便起见,将其包装成一个类,通过初始化来改变神经网络的层数,也就是两层和多层神经网络共用一套代码。
二、编程实现
1.数据处理
数据处理这部分和第二周编程作业一致,首先读取 ==.h5== 文件中的数据(dataset中的数据信息我放在文末的百度网盘链接中):
import numpy as np
import h5py
def load_dataset():
train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
classes = np.array(test_dataset["list_classes"][:]) # the list of classes
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes每张图片的大小为64*64像素,而每个像素点由RGB三原色组成,所以每张图片的数据维度为(64,64,3),所以一张图片需要12288个数据确定。
train_set_x_orig:训练集图像数据,一共209张,数据维度为(209,64,64,3)
train_set_y_orig:训练集的标签集,维度为(1,209)
test_set_x_orig:测试集图像数据,一共50张,维度为(50,64,64,3)
test_set_y_orig:测试集的标签集,维度为(1,50)
classes : 保存的是以bytes类型保存的两个字符串数据,数据为:[b’non-cat’ b’cat’]我们知道逻辑回归的输入x一般是一维向量,我们需要对 ==train_set_x_orig== 和 ==test_set_x_orig== 进行处理,从(209,64,64,3) 转换为(12288,209)维度,可以利用numpy库中的reshape()方法完成。numpy的shape通常返回一个元组,比如这里的 ==train_set_x_orig.shape== 返回的元组为(209,64,64,3),所以==train_set_x_orig.shape[0]== 的值为 ==209== 。
def data_preprocess():
"""
数据预处理
:return:
train_set_x -训练集(12288,209)
train_set_y -训练集标签(1,209)
test_set_x -测试集(12288,50)
test_set_y -测试集标签(1,50)
"""
# 获得训练集209条数据和测试集50条数据
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
plt.imshow(train_set_x_orig[27])
plt.show()
# 每一张图片是64*64*3(这里的64*64表示像素点个数,3表示每个像素点由RGB三原色构成),将其转换成列向量
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T # 得到训练集输入数据,维度为(64*64*3,209)
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T # 得到测试集输入数据,维度为(64*64*3,50)
# RGB的取值为(0,255),需要将数据进行居中和标准化,将数据集的每一行除以255(一般是将每一行数据除以该行数据的平均值)
train_set_x = train_set_x_flatten / 255
test_set_x = test_set_x_flatten / 255
return train_set_x, train_set_y, test_set_x, test_set_y2.初始化神经网络参数
我以类的方式初始化一个神经网络:
class NeuralNetwork(object):
def __init__(self, input_num, hidden_num, output_num, activation, learning_rate):
self.W = [0]
self.b = [0]
self.A = []
self.Z = [0]
self.learning_rate = learning_rate
self.input_layer = input_num
self.hidden_num = hidden_num
self.output_num = output_num
self.activation = activation
self.initialize_parameters()我们先来看看需要传入的参数。
1.input_num:输入层神经元数量,整型。
2.hidden_num:各个隐藏层神经元数量,整型列表。
3.output_num:输出层神经元的数量,整型。
4.activation:激活函数类型(relu或sigmoid),字符串列表。
5.learning_rate:学习率。这里我将输入层,隐藏层,输出层的维度分开输入,也可以放到一个列表中输入。我们再来看看类的一些成员变量:
1.W,b:神经网络的参数。
2.A,Z:每层神经元的激活值。W列表的0号位置初始化为0,是为了方便后面的运算。当我们将参数传入后,需要初始化权重矩阵W和偏移向量b:
def initialize_parameters(self):
"""
初始化w,b矩阵
:return:
"""
for l in range(0, len(self.hidden_num)):
if l == 0:
W = np.random.randn(self.hidden_num[l], self.input_layer) * 0.01
b = np.zeros((self.hidden_num[0], 1))
else:
W = np.random.randn(self.hidden_num[l], self.hidden_num[l - 1]) * 0.01
b = np.zeros((self.hidden_num[l], 1))
self.W.append(W)
self.b.append(b)
W = np.random.randn(self.output_num, self.hidden_num[-1])
b = np.zeros((self.output_num, 1))
self.W.append(W)
self.b.append(b)关于W和b的初始化,b默认初始化为0,而W却是随机数。起初我并未将W的值乘上0.01进行平衡导致计算得到的损失值为nan,这是因为W初始化的值较大,使得计算得到的Z的值较大,最后的输出层结果十分接近0或1,使得计算cost时出了问题。
3.前向传播
这里我们将前向传播分为两部分计算:
1.线性部分:Z=WA+b
2.非线性部分:A=sigmoid(Z)或A=relu(Z)3.1线性前向传播
def forward_linear(self, W, b, X):
"""
前向传播线性部分,计算a=wx+b
:param X: 输入数据
:param W:权重矩阵
:param b:偏移向量
:return:
"""
Z = np.dot(W, X) + b
assert (Z.shape == (W.shape[0], X.shape[1]))
return Z函数的输入包括输入数据X,权重矩阵W,和偏移向量b。其实类成员中保存了W和b的值,我们只需要传入当前需要计算的层的序号L即可。
3.2非线性+线性前向传播
def activation_linear_forward(self, L):
"""
整体激活函数,先线性激活,在用激活函数非线性激活
:param L: 前一层的输出
:return:
"""
activation = self.activation[L]
Z = self.forward_linear(self.W[L], self.b[L], self.A[L - 1])
self.Z.append(Z)
if activation == "sigmoid":
A = sigmoid(Z)
elif activation == "relu":
A = relu(Z)
self.A.append(A)先通过线性部分的计算得到Z的值,然后根据当前层的激活函数得到非线性的值A,这样就得到了当前层的输出,将A和Z的值保存起来,供后面的反向传播使用。激活函数sigmoid和relu的程序如下:
def sigmoid(Z):
"""
Implements the sigmoid activation in numpy
Arguments:
Z -- numpy array of any shape
Returns:
A -- output of sigmoid(z), same shape as Z
"""
A = 1/(1+np.exp(-Z))
return A
def relu(Z):
"""
Implement the RELU function.
Arguments:
Z -- Output of the linear layer, of any shape
Returns:
A -- Post-activation parameter, of the same shape as Z
efficiently
"""
A = np.maximum(0,Z)
assert(A.shape == Z.shape)
return A3.3 前向传播主控程序
def model_forward(self, X):
"""
正向传播主控函数,输入数据x得到神经网络的最终输出
:param X: 输入数据
:return:
"""
self.A = [X]
self.Z = [0]
for l in range(1, len(self.hidden_num) + 2):
self.activation_linear_forward(l)4.反向传播
反向传播我也分为两部分计算:线性和非线性。
4.1线性反向传播
1.dA[L]=np.dot(W[L+1].T, dZ)
2.dW[L]=(1/m)*(np.dot(dZ,A[L-1].T))
3.db[L]=np.sum(dZ,axis=1,keepdim=True) """
反向传播线性部分,计算dw,db和da
:param dZ:相对于(当前第l层的)线性输出的成本梯度
:param L:当前层数
:return:
"""
m = self.A[L - 1].shape[1]
dW = np.dot(dZ, self.A[L - 1].T) / m
db = np.sum(dZ, axis=1, keepdims=True) / m
dA_pre = np.dot(self.W[L].T, dZ)
return dA_pre, dW, db4.2非线性+线性反向传播
def linear_activation_backward(self, dA, L):
"""
完整的反向传播,线性+非线性
:param dA: L层A的梯度值
:param L:当前层
:return:
"""
activation = self.activation[L]
if activation == "relu":
dZ = relu_backward(dA, self.Z[L])
dA_pre, dW, db = self.linear_backward(dZ, L)
elif activation == "sigmoid":
dZ = sigmoid_backward(dA, self.Z[L])
dA_pre, dW, db = self.linear_backward(dZ, L)
return dA_pre, dW, db非线性部分求dZ涉及到激活函数求导问题,这里将其封装成函数 ==relu_backward== 和 ==sigmoid_backward== 。
def sigmoid_backward(dA, cache):
"""
Implement the backward propagation for a single SIGMOID unit.
Arguments:
dA -- post-activation gradient, of any shape
cache -- 'Z' where we store for computing backward propagation efficiently
Returns:
dZ -- Gradient of the cost with respect to Z
"""
Z = cache
s = 1/(1+np.exp(-Z))
dZ = dA * s * (1-s)
assert (dZ.shape == Z.shape)
return dZ
def relu_backward(dA, cache):
"""
Implement the backward propagation for a single RELU unit.
Arguments:
dA -- post-activation gradient, of any shape
cache -- 'Z' where we store for computing backward propagation efficiently
Returns:
dZ -- Gradient of the cost with respect to Z
"""
Z = cache
dZ = np.array(dA, copy=True) # just converting dz to a correct object.
# When z <= 0, you should set dz to 0 as well.
dZ[Z <= 0] = 0
assert (dZ.shape == Z.shape)
return dZ4.3反向传播主控函数
主控函数主要完成两个工作:1.反向传播求得各参数的梯度。2.根据求得的梯度和学习率更新各个参数。
def model_backward(self, Y):
"""
反向传播主控程序,计算参数梯度并更新
:return:
"""
A = self.A[-1]
dA = - (np.divide(Y, A) - np.divide(1 - Y, 1 - A))
L = len(self.W)
for l in range(L-1, 0, -1):
dA, dW, db = self.linear_activation_backward(dA, l)
self.W[l] = self.W[l] - self.learning_rate * dW
self.b[l] = self.b[l] - self.learning_rate * db5.损失函数
def compute_cost(self, Y):
"""
计算代价函数的值
:param Y: 样本的实际标签值
:return: cost-交叉熵成本
"""
m = Y.shape[1]
cost = (-1) * np.sum(np.multiply(np.log(self.A[-1]), Y) + np.multiply(np.log(1 - self.A[-1]), 1 - Y)) / m
cost = np.squeeze(cost)
return cost6.预测函数
def predict(self, X, y):
"""
该函数用于预测L层神经网络的结果,当然也包含两层
参数:
X - 测试集
y - 标签
返回:
p - 给定数据集X的预测
"""
m = X.shape[1]
p = np.zeros((1, m))
# 根据参数前向传播
self.model_forward(X)
for i in range(0, self.A[-1].shape[1]):
if self.A[-1][0, i] > 0.5:
p[0, i] = 1
else:
p[0, i] = 0
print("准确度为: " + str(float(np.sum((p == y)) / m)))
return p
三、测试
初始化为两层神经网络:
train_set_x, train_set_y, test_set_x, test_set_y = data_preprocess()
costs = []
# activation = [0, "relu", "relu", "relu", "sigmoid"]
num_iteration = 2500
activation = [0, "relu", "sigmoid"]
learning_rate = 0.0075
# hidden_layer = [20, 7, 5]
hidden_layer = [7]
nn = NeuralNetwork(12288, hidden_layer, 1, activation, learning_rate)
for i in range(0, num_iteration):
nn.model_forward(train_set_x)
nn.model_backward(train_set_y)
cost = nn.compute_cost(train_set_y)
if i % 100 == 0:
costs.append(cost)
print("第 ", i, " 次循环,成本为:" + str(cost))
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
print("训练集准确率:"+str(nn.predict(train_set_x, train_set_y)))
print("测试集准确率:"+str(nn.predict(test_set_x, test_set_y)))结果如下:
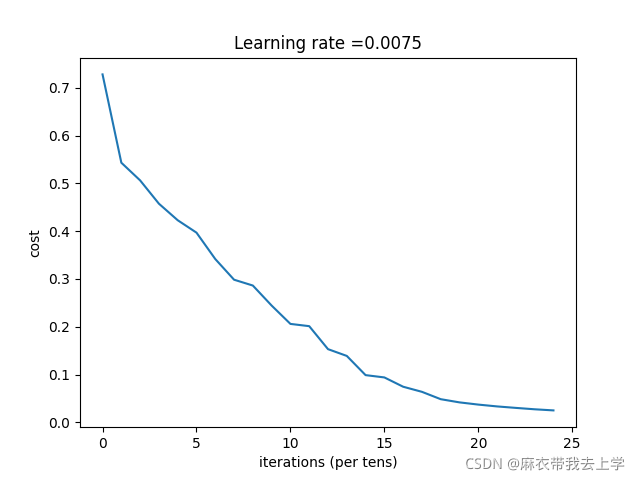

搭建多层神经网络:
if __name__ == "__main__":
train_set_x, train_set_y, test_set_x, test_set_y = data_preprocess()
costs = []
activation = [0, "relu", "relu", "relu", "sigmoid"]
num_iteration = 2500
# activation = [0, "relu", "sigmoid"]
learning_rate = 0.0075
hidden_layer = [20, 7, 5]
# hidden_layer = [7]
nn = NeuralNetwork(12288, hidden_layer, 1, activation, learning_rate)
for i in range(0, num_iteration):
nn.model_forward(train_set_x)
nn.model_backward(train_set_y)
cost = nn.compute_cost(train_set_y)
if i % 100 == 0:
costs.append(cost)
print("第 ", i, " 次循环,成本为:" + str(cost))
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
print("训练集准确率:"+str(nn.predict(train_set_x, train_set_y)))
print("测试集准确率:"+str(nn.predict(test_set_x, test_set_y)))总结
这里我只给出了双层神经网络的结果测试,效果还是不错的。但是当我用相同的代码构建多层神经网络时效果就非常差,我目前还在学习过程中,并没有发现问题出在哪里。我把代码已经上传到百度网盘中,提取码:8jb2。希望有大神能给我一些指导意见,万分感谢。

