一、mini-batch梯度下降

向量化样本数据能够帮助我们同时计算多个样本，例如每个样本的特征数为50，样本数为100，我们可以构造样本数据矩阵(50，100)，将矩阵输入到神经网络中就可以同时计算100个样本数据的输出值，神经网络输出值的维度为(1，100)。

$$
\begin{aligned}
input:X(n_x,m),n_x为特征数,m为样本数\
\end{aligned}
$$

$$
\begin{aligned}
output:Y(1,m)\
\end{aligned}
$$

当数据量很少时，向量化输入数据确实能帮助我们相对较快地处理样本，但是样本数据量较大时，比如50万或者500万，输入矩阵就会变得特别庞大，效果可能会适得其反。这时我们需要设置常说的batch size，batch size的值表示着神经网络一次需要处理的样本数量。例如，当样本数量为50万时，设置batch size的值为1000，则神经网络每次需要处理的样本数量为1000，即输入数据的矩阵维度为(nx，1000)，神经网络需要处理500个这样的数据。

根据batch size的大小，可以做出简单的分类：

1.batch_size=m，一次训练整个训练集，称为batch梯度下降法
2.batch_size=1，称为随机梯度下降法
3. 1<batch_size<m，称为mini-batch梯度下降法

需要注意的是，在mini-batch梯度下降中，神经网络每处理完一个batch都需要进行反向传播。例如，当样本数50万，batch size为1000时，每一轮训练（一轮训练是指遍历完所有样本）需要进行500次反向传播。这就使得绘制得到的loss曲线可能并不是很光滑，会存在一些噪声，但是整体趋势是下降的。

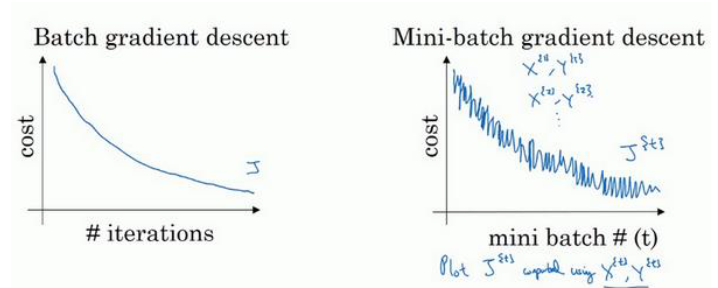
关于batch size大小的选择，考虑到电脑内存的设置和使用方式通常来说是2的n次方，比如64，128等，当然这和CPU和GPU的性能有关。另外当样本数据较少时，并不建议使用mini-batch梯度下降法，batch梯度下降法可能效果会更好。

二、指数加权平均数(Exponentially weighted averages)

为了更好理解之后的优化算法，需要了解指数加权平均数的概念，我们从一个简单的例子来介绍指数加权平均数。

上图是某地一年天气的散点图，横坐标是日期，纵坐标是温度。我们知道每一天的气温的具体数值(用𝜃1,𝜃2,...𝜃t表示)，可以做如下运算：
$$
\begin{aligned}
v_0=0
\end{aligned}
$$

$$
v_1=0.9v_0+0.1\theta_1
$$

$$
v_2=0.9v_1+0.1\theta_2
$$

$$
......
$$

$$
vt=0.9v{t-1}+0.1\theta_t
$$
通过这样的计算我们其实得到了移动平均值，用红线作图的话，可以得到下面的结果：

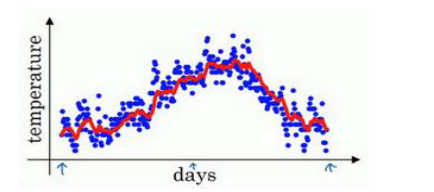
更加一般的计算公式是：
$$
vt=\beta v{t-1}+(1-\beta)\theta_t\
$$

$$
v_t可以看作\frac{1}{1-\beta}天的平均气温
$$
因此𝛽=0.9时，求得的vt相当于近十天的气温平均数。同理当𝛽=0.98时，则平均了近50天的平均气温（如下图绿线所示），𝛽=0.5则是平均了近两天的气温（如下图黄线所示）。

可以看出，当𝛽值越大时得到的曲线约平缓，当𝛽值越小时得到的曲线越陡峭。指数加权平均数在初期计算时其实不太准确，由于v0等于0，那么计算v1其实是特别不准确的，尤其是当𝛽特别大的时候。

因此我们常采用偏差修正的手段使得平均数的计算更加准确，还是以𝛽=0.98进行解释，原始指数加权平均数的计算过程为：
$$
v_0=0
$$

$$
v_1=0.98v_0+0.02\theta_1=0.02\theta_1
$$

$$
v_2=0.98v_1+0.02\theta_2=0.0196\theta_1+0.02\theta_2
$$

加入偏差修正后的计算过程：
$$
用\frac{v_t}{1-\beta^t}代替v_t
$$

$$
t=2:1-\beta^t=1-0.98^2=0.0396
$$

$$
\frac{v_2}{0.0396}=\frac{0.0196\theta_1+0.02\theta_2}{0.0396}
$$

随着t的增加𝛽^t逐渐接近于0，这就使得偏差修正只在指数加权平均数计算的初期起作用。

三、动量梯度下降法(Gradient descent with Momentum)

在了解了指数平均加权数计算过程后，我们来看一下动量梯度下降法是如何实现的。动量梯度下降法运行速度几乎总是快于标准的梯度下降法，其基本思想是利用梯度的指数加权平均数来更新权重。

当损失函数曲线较为狭长时，如下图所示，利用mini-batch或者其他标准的梯度下降法，会使得趋近最小值的过程十分振荡。这时如果增大学习率会使得纵轴方向的波动更加剧烈（如紫线所示），不能通过简单地增加学习率达到加快训练的速度。

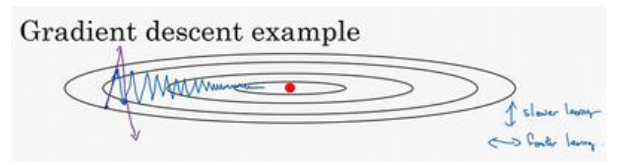
而动量梯度下降法的计算步骤是：
$$
v{dW}=\beta v{dW}+(1-\beta)dW
$$

$$
v{db}=\beta v{db}+(1-\beta)db\
$$

$$
W=W-\alpha v_{dW}
$$

$$
b=b-\alpha v_{db}
$$

在纵轴方向波动表明，纵轴方向代表的参数的偏导数时正时负，通过指数加权平均数来计算该参数的偏导数，可以使得该参数的偏导数更趋向于0，至少不会时正时负。而横轴方向的偏导数并不存在这个问题，这时增加学习率可以加快趋近最小值的过程。

这里并未加入偏差修正的操作，加上后效果应该更好。另外，动量梯度下降法可以和标准的梯度下降法结合使用。使用动量梯度下降法后，这里存在两个超参数𝛽和𝑎，𝑎就是我们熟知的学习率，而𝛽的通常取值为0.9。

在代码实现方面其实并不复杂，我们只是在传统的梯度下降法的参数更新上增加了两个公式的计算，反应在代码上只是多了两三行代码。

四、RMSprop(Root Mean Square prop)

RMSprop算法和动量梯度下降算法一样，也是在参数更新的地方做了一些“手脚”，RMSprop算法的更新参数的方程为：
$$
S{dW}=\beta S{dW}+(1-\beta)(dW)^2\
$$

$$
S{db}=\beta S{db}+(1-\beta)(db)^2\
$$

$$
W=W-\alpha \frac{dW}{\sqrt{S_{dW}}}\
$$

$$
b=b-\alpha \frac{db}{\sqrt{S_{db}}}
$$

还是以动量梯度下降法中的例子来进行说明，假设纵轴代表着参数b，横轴代表着参数W。由于平方操作使得db的正负性失去了意义，但是在纵轴上波动较大证明db的绝对值较大，因此S_db较大，b更新的变化较小。同理，横轴方向变化较小，因此dW较小，SdW较小，W更新变化较大。这就使得，纵轴摆动变小，横轴速度加快，加速了训练的过程，如下图绿线所示。

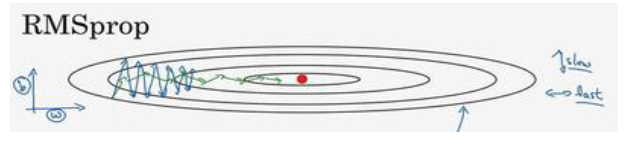
五、Adam优化算法

Adam优化算法其实就是动量梯度下降法和RMSprop算法的一个结合，具体计算步骤如下：

$$
初始化：V{dW}=0,S{dW}=0,V{db}=0,S{db}=0\
$$

$$
V_{dW}=\beta1V{dW}+(1-\beta1)dW，V{db}=\beta1V{db}+(1-\beta_1)db\
$$

$$
S_{dW}=\beta2S{dW}+(1-\beta2)(dW)^2，S{db}=\beta2S{db}+(1-\beta_2)(db)^2\
$$

$$
偏差修正：\
$$

$$
V{dW}^{correct}=\frac{V{dW}}{1-\beta1^t}，V{db}^{correct}=\frac{V_{db}}{1-\beta_1^t}\
$$

$$
S{dW}^{correct}=\frac{S{dW}}{1-\beta2^t}，S{db}^{correct}=\frac{S_{db}}{1-\beta_2^t}
$$

$$
参数更新：\
$$

$$
W=W-\alpha(\frac{v{dW}^{correct}}{\sqrt{S{dW}^{correct}+\epsilon}})，b=b-\alpha(\frac{v{db}^{correct}}{\sqrt{S{db}^{correct}+\epsilon}})
$$

$$
(\epsilon 是防止分母为0而添加的极小项，一般为10^{-8}）
$$

Adam算法涉及到的超参数很多，除了学习率需要自己调试外，其他超参数都有参考值：
$$
\beta_1=0.9，\beta_2=0.999，\epsilon=10^{-8}
$$
从计算过程可以看出，Adam算法是RMSprop算法和动量梯度下降法的一个融合，看起来很复杂其实转换成代码后并不复杂，另外，一些深度学习框架都将这些优化算法封装的比较完善，方便我们使用。

六、学习率衰减(Learning rate decayf)

使用mini-batch梯度下降法时，在迭代过程中会有噪音，下降会朝向最小值，但是不会精确地收敛（如下图蓝线所示），因为使用的学习率是固定值。梯度下降初期可能需要较大的学习率加快收敛，但是到最小值附近时大的学习率反而不利于收敛，导致最后会在最小值附近大幅摆动。因此我们希望学习率是可变的，初期学习率较大，后期学习率相对较小，收敛更加顺利（如下图绿线所示）。

学习率衰减算法就是使用的动态学习率，具体计算公式如下：
$$
\alpha=\frac{1}{1+decay_rate*epoch_num}\alpha_0
$$
其中decay-rate称为衰减率，epoch-num是迭代轮数（遍历所有训练样本为1轮），𝑎0为初始学习率。