一、神经网络中的超参数
根据吴恩达老师深度学习视频,按重要性给神经网络中的超参数排个序:
- 学习率α
- 动量梯度下降中的β,隐藏单元数hidden_units,批处理大小mini_batch_size
- 层数layers,学习率衰减参数learning_rate_decay
一个好的神经网络难免会经过多次调参,吴恩达老师给出的调参策略是,先随机选取多组参数的数值,找到表现效果较好的一组,再找这组附近的值。
二、Batch Normalization(BN)
在之前的学习中我们知道,为了加快神经网络训练,往往会采用归一化的方式。通过零均值和归一化方差的操作,使得样本分布更加均匀,代价函数图像也更加圆形化,更易于梯度下降。
BN也是通过零均值和归一化方差来处理数据,与之前提到的归一化不同,BN作用于神经网络的内部。我们知道,神经网络的第L层的输入是第(L-1)层的输出,用a[L-1]表示,将a[L-1]归一化后再输入到第L层,其实会更加有效地训练第L层的参数W[L]和b[L]。这就是BN的一个大致思路,落实到具体实现时,我们往往不是归一化a[L-1],而是归一化z[L],也就是说,第L层接收到第(L-1)层的输出后,先线性激活再归一化。对于第l层具体计算公式为:
$$
Z^{[l]} = W^{[l]}a^{[l-1]}+b^[l]\
$$
$$
\mu = \frac{1}{m}\sum_{i}(z^{[l][i]}-\mu)\
$$
$$
\sigma^2=\frac{1}{m}\sum_{i}(z^{[l][i]}-\mu)\
$$
$$
Z^{[l]}_{norm}=\frac{Z^{[L]}-\mu}{\sqrt{\sigma^2+\epsilon}}(\epsilon为防止分母为0)\
$$
以上就是把𝑧值标准化的过程,化为含平均值 0和标准单位方差,所以𝑧的每一个分量都含有平均值 0和方差 1,但我们不想让隐藏单元总是含有平均值 0和方差 1,也许隐藏单元有了不同的分布会有意义。因此我们接下来的操作是:
$$
\tilde{Z^{[l]}}=\gamma^[l]Z^{[l]}_{norm}+\beta^{[l]}\
a^{[l]}=g(\tilde{Z}^{[l]})
$$
$$
a^{[l]}=g(\tilde{Z}^{[l]})
$$
这里我们引入了两个参数𝛾和𝛽,这两个参数和w一样是需要学习的,同样可以对𝛾和𝛽使用动量梯度下降或是Adam优化算法,并且每一层都会有独立的𝛾和𝛽。
这里还需要注意一个问题,神经网络训练时往往一次处理多个样本数据,也就是所谓的batch_size,batch_size的值通常不是1,因此每层对Z进行求方差和均值是有意义的。但是当模型训练完成后,难免会处理单个样本,这时方差和均值就没有意义。因此,我们通常的做法是求均值和方差的指数加权平均数,具体参考上一篇博客中的介绍。
三、Softmax回归
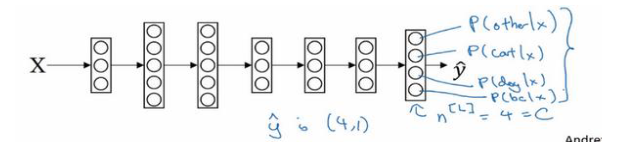
如果要搭建神经网络处理二分类问题,通常的做法是在输出层设置一个神经元并使用sigmoid激活函数。那么如果要处理多分类问题时,应该怎么做呢?一般而言我们在输出层使用softmax完成多分类,输出层的神经元个数由分类个数来设置,以四分类为例,神经网络的结构可以为:
softmax做的操作是:
$$
t=e^{(Z^{[l]})}\
$$
$$
a^{[l]}=\frac{e^{(Z^{[l]})}}{\sum_{j=1}^{C}t_j},a^{[l]}_i=\frac{ti}{\sum\{j=1}^{C}t_j}(C为类别数)
$$
通过公式可以看出,输出层的向量a的各元素之和为1,因此a中各元素可以看作属于各个分类的概率。
在使用softmax处理多分类问题时,我们需要对标签值进行处理。通常来说,多分类的标签值是一个具体数值,而我们需要将其转化为one-hot的形式,比如说,在四分类中,一个样本的标签值为3,则需要转化为[0,0,1,0]向量形式。确定好样本标签形式后,softmax的损失函数为:
$$
L(\hat{y},y)=-\sum_{j=1}^Cy_jlog\hat{y}_j
$$
以标签值为3的样本为例:
$$
y=[0,0,1,0]^T\
$$
$$
L(\hat{y},y)=-y_3log\hat{y}_3=-log\hat{y}_3
$$
要想减少loss值,则需要增大神经网络输出层在第三个神经元的输出值,也就是增大样本属于第三类的可能性,这与我们的预期相同。