一、训练集、验证集和测试集的划分
在机器学习发展的小数据时代,常见做法是将所有数据三七分,即70%训练集和30%测试集,如果没有明确设置验证集,也可以按照60%训练集,20%验证集,20%测试集来划分。 这是早些年机器学习领域普遍认可的最好的实践方法,如果数据只有100条,1000条或10000条,上述比例是非常合理的。
但是在大数据时代,我们现在的数据量可能是百万级别,那么验证集和测试集占数据总量的比例会趋向于变得更小。因为验证集的目的就是为了验证不同的算法,检验哪种算法更有效,我们不需要拿出20%的数据作为验证集。
在这里给出一个结论,在机器学习中,我们通常将样本分成训练集,验证集和测试集三部分,数据集规模相对较小,适合传统的划分比例,数据集规模较大的,验证集和测试集要小于总量的20%或10%。
还有一点需要注意的是,确保测试集和验证集的数据来自同一分布。庞大的数据往往来源不止一个,比如说,现在需要收集猫的图片,我们可以从高清网站上爬取,也可以请业余人士手机拍摄,前者得到的照片像素高,清晰度高,后者得到的照片质量相比之下就没有那么好,这种情况下,需要避免测试集和验证集中的数据来自两个分布。训练集来自专业网站,测试集和验证集来自业余人士手机拍摄。
二、偏差和方差(Bias & Variance)
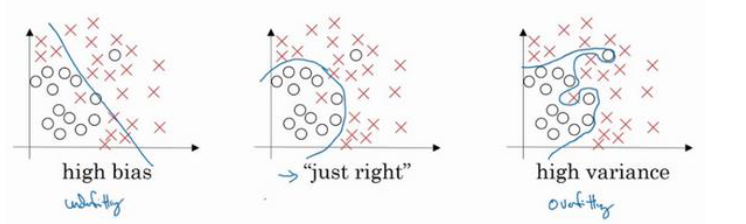
熟悉机器学习的应该知道,这三种方案的拟合情况是:欠拟合,正常拟合和过拟合。对偏差和方差的一个直观理解是,欠拟合(underfitting)代表着高偏差(high bias),过拟合(overfitting)代表着高方差(high variance)。
如果通过模型在训练集和验证集上的误差来判断偏差和方差的话,简单来说就是:
1.训练集上误差低,验证集上误差高=》高方差(high variance)
2.训练集和验证集误差都高,但是二者相近=》高偏差(high bias)
3.训练集和验证集误差都高,但是验证集误差明显高于训练集=》高偏差和高方差偏差更倾向于衡量模型在训练集上的表现效果,方差更倾向于衡量模型在验证集或测试集上的表现效果。
三、避免高偏差和高方差的一些策略
避免高偏差(high bias)的的策略:
1.评估训练集或训练数据的性能是否合理
2.采取新的神经网络结构,或增加隐藏层和隐藏单元,用更大的网络去拟合训练数据
3,增加训练时间,优化算法(增加训练时间不一定有效,但是至少没什么坏处)避免高方差(high variance)的策略:
1.评估验证集的性能是否合理
2.增加训练集,提高模型的性能
3.正则化上述的策略来自吴恩达老师深度学习视频,大多都是通过大量实践得到的经验,不一定保证有效,但是值得尝试。
四、L2正则化(L2 Regularization)
正则项一般作用于代价函数,以逻辑回归为例,代价函数正则化得到的公式如下:
$$
J(W,b)=\frac{1}{m}\sum_{i=1}^m L(\hat{y^{(i)}},y^{(i}) + \frac{\lambda}{2m}||W||^22+ \frac{\lambda}{2m}\sum{l=1}^L||W^{[l]}||_F^2
$$
这就是L2正则化,最后一项为权重矩阵W的L2范数(也称为欧几里得范数),具体的计算为:
$$
||W||^22=\sum{j=1}^{m}wj^2=W^TW
$$
对应的也有L1正则化,但是使用的比较少,这里给出L1正则化的正则项:
$$
\begin{aligned}
\frac{\lambda}{m}|W| && |W|=\sum{j=1}^{n}w_j
\end{aligned}
$$
L1正则化会使得W矩阵变得稀疏,有人认为这可以用于压缩模型,但是很少有人这么用,因此人们在训练网络时越来越倾向于使用L2正则化,这里就不再过多讨论L1正则化。为什么只正则化参数W?无论是逻辑回归还是神经网络,需要更新的参数主要是W,相较于W,偏移量b占比比较少,因此添加参数b实际作用不大。
接下来看看神经网络中的正则化:
$$
\begin{aligned}
J(W^{(1)},b^{(1)},W^{(2)},b^{(2)},...,W^{(L)},b^{(L)})=\frac{1}{m} \sum{i=1}^{m}L(\hat y^{(i)},y^{(i)})
\end{aligned}
$$
$$
\begin{aligned}
||W^{[l]}||{F}^{2}=\sum^{n^{[l-1]}}_{i=1}\sum_{j=1}^{n^{[l]}}(w_{ij}^{[l]})
\end{aligned}
$$
可以看出,神经网络正则化公式与逻辑回归正则化公式大致相似,只是在神经网络中,两层之间的权重参数都是一个矩阵,因此求L2范式时需要单独求每个权重矩阵的L2范式并求和。顺带一提的是,我们通常不将该正则项称为L2范数,而是称为“弗罗贝尼乌斯范数”,它表示一个矩阵中所有元素的平方和。
既然添加正则化后损失函数的表达式发生了变化,那么对应反向传播过程方程也需要做出修改。幸运的是,添加正则项后公式的变化并不复杂,只需要再原来反向传播的基础上加上正则项的导数即可:
$$
\begin{equation}
dw^{[l]}=(from_{}backprop)+\frac{\lambda}{m}w^{[l]}
\end{equation}
$$
五、正则化为什么会起作用
关于正则化为什么会起作用的问题,是存在一套严格的证明方法,这里给出一个直观的解释,不存在公式推导(严格的公式推导博主也不会😅)。
我们知道正则化是为了解决模型过拟合而采取的一个手段,模型过拟合的一个原因是模型参数过多,产生的决策边界函数曲线完美分割训练集中的样本,甚至是一些错误样本也能分割(具体可以参考上文中的过拟合示例图),得到的模型的泛化性能力不强,在验证集或是测试集上表现效果较差。
既然知道问题出在模型参数过多,那么适当减少模型中的参数就可以减轻过拟合现象。这里考虑一个极端的情况,假如正则项中的λ非常大导致第一项中损失函数的作用微乎其微,那么反向传播更倾向于减少正则项的结果,这就导致一些神经元的权重值会变为0,这就变相使得一些神经元失活,减少模型的参数,防止过拟合。其实,有些模型会设置dropout参数,每一轮训练完成时会使一些神经元失活,防止过拟合。
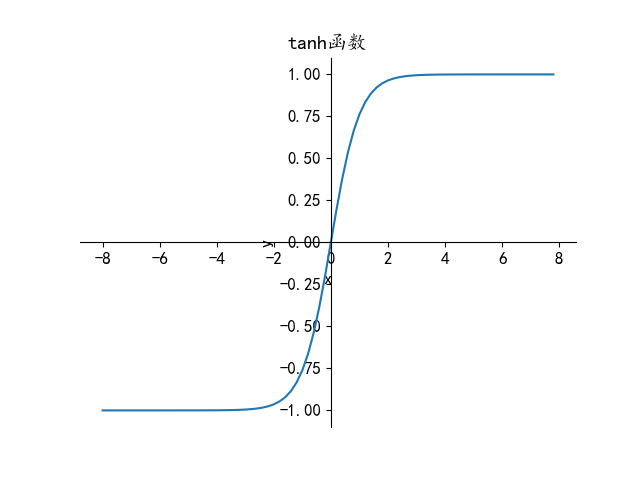
从激活函数来看,更加直观的解释就是,正则项的加入使得神经元的权重值w加速减小,当λ足够大时,某些神经元的w值会变得接近于0,以tanh函数为例:
$$
z=wa^{[l]}+b \text{,线性激活} \
a^{[l+1]}=tanh(z)\text{,非线性激活}
$$
w减小会导致z的变小,从tanh图像可以看出,当x较小时,图像大致呈线性,我们知道线性网络是无法产生出复杂的决策边界,从而阻止了过拟合。
六、Dropout正则化(Dropout Regularization)
Dropout正则化的中心思想是“随机失活”,最常用的方法是inverted dropout(反向随机失活),大致步骤如下:
1.随机初始化一个d[l]向量,l为层的编号,因此每一层(或者说每两层之间)都对应有一个d[l]向量,例如:
d3 = np.random.rand(a3.shape[0],a3.shape[1])
2.设置评判标准𝑘𝑒𝑒𝑝−𝑝𝑟𝑜𝑏,𝑘𝑒𝑒𝑝−𝑝𝑟𝑜𝑏为一个具体数字,表示保留一个隐藏单元的概率。假设为0.8,则d[l]中值为1的概率为0.8,为0的概率为0.2,例如:
d3 = np.random.rand(a3.shape[0],a3.shape[1])<0.8
3.得到l层的输出a[l],将a[l]与d[l]相乘,例如:a3 =np.multiply(a3,d3)
4.𝑎3/=𝑘𝑒𝑒𝑝−𝑝𝑟𝑜𝑏 关于第2步,我们初始化的d向量是通过numpy的提供的随机数函数rand完成的,这就表明d向量中的值实在0~1之间均匀分布的,小于0.8的值占80%,大于0.8的值占20%,通过d3 = np.random.rand(a3.shape[0],a3.shape[1])<0.8可以使得d向量中80%的值变为true,20%的值变为false,python会自动将true处理成1,false处理成0进行运算。
第4步的意义在于,经过第3步后,a[l]中每个值舍弃的概率为0.2,a[l]的期望减少了20%,因此第4步是为了不影响下一层的输出结果而进行的操作。
关于d向量的初始化问题:每进行一轮新的训练,d向量需要重新初始化。这就导致有时这个神经元会被删除,有时这个神经元不会被删除。这就使得神经网络不会将重心放在一个神经元节点上,不会给一个神经元赋予更大的权重。
另外每层𝑘𝑒𝑒𝑝−𝑝𝑟𝑜𝑏的值可以不一样,当𝑘𝑒𝑒𝑝−𝑝𝑟𝑜𝑏的值设置成1时,表明不会在这层实行dropout操作。
七、归一化输入(Normalization)
训练神经网络时,我们可以通过归一化输入加速神经网络训练。归一化主要分为两个步骤:零均值和归一化方差。
$$
\mu=\frac{1}{m}\sum{i=1}^mX^{(i)},X=X-\mu \text{(零均值)}\
\sigma^2=\frac{1}{m}\sum{i=1}^m(X^(i))^2,X=\frac{X}{\sigma^2}{(归一化方差)}
$$
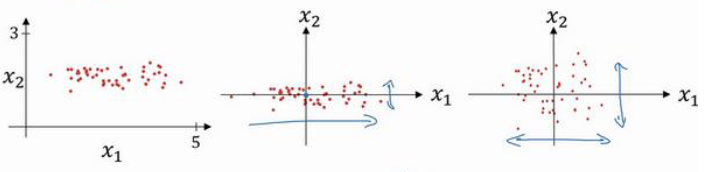
通过三张图来大致了解归一化的过程,第一张图时未经处理的数据,当我们进行零均值后得到第二张图,可以看出,零均值的意义在于移动数据集,让其更靠近于中心点分布。回到数据集本身,可以看出数据集在x1反向上的反差要远大于x2方向上的方差,方差归一化后的结果第三张图所示,数据集在x1方向和x2方向上的方差大致相同。
那么归一化的意义在哪呢?归一化主要通过加速梯度下降的过程来加快模型训练:
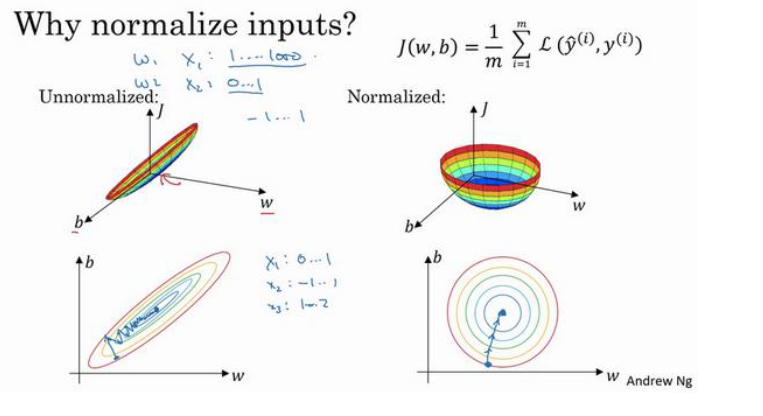
归一化后使得代价函数的图像更加原型化,相较于未归一化的较为狭长的代价函数,圆形化的代价函数梯度下降得更快,更容易找到最小值。
