前言

本系列主要是对pytorch基础知识学习的一个记录，尽量保持博客的更新进度和自己的学习进度。本人也处于学习阶段，博客中涉及到的知识可能存在某些问题，希望大家批评指正。另外，本博客中的有些内容基于吴恩达老师深度学习课程，我会尽量说明一下，但不敢保证全面。

一、问题描述

此次需要构建的神经网络其实和前几次相同，为了能更直观的理解问题，绘制了一张精美的神经网络结构图：

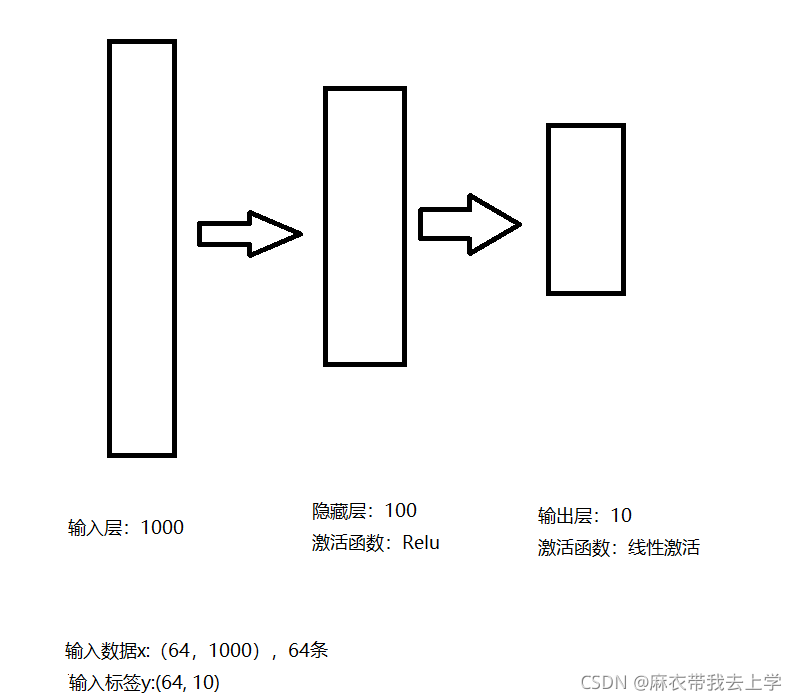
二、官方代码

因为代码量确实很少，在这里一次性贴上全部代码。

import torch

N, D_in, H, D_out = 64, 1000, 100, 10

x = torch.randn(N, D_in)
y = torch.randn(N, D_out)

model = torch.nn.Sequential(torch.nn.Linear(D_in, H),
                            torch.nn.ReLU(),
                            torch.nn.Linear(H, D_out))

loss_fn = torch.nn.MSELoss(reduction='sum')

learning_rate = 1e-4

for t in range(500):
    #前向传播
    y_pred = model(x)

    #计算损失函数
    loss = loss_fn(y_pred, y)
    print(t, loss.item())

    #将梯度清零
    model.zero_grad()

    #反向传播
    loss.backward()

    #梯度更新
    with torch.no_grad():
        for param in model.parameters():
            param -= learning_rate * param.grad

可以看出，构建相同结构的神经网络，使用nn模块编程比不使用nn模块编程更为简洁，更不用提使用numpy编程了。

三、代码讲解

1.参数初始化

在上述代码中，我们很明显的察觉到并没有对各层的权重矩阵w进行初始化。在之前使用pytorch的自动求导时，我们需要初始化权重矩阵，并需要将requires_grad的值设为True，代码如下：

w1 = torch.randn(D_in, H, device=device, dtype=dtype, requires_grad=True)
w2 = torch.randn(H, D_out, device=device, dtype=dtype, requires_grad=True)

而使用nn模块后，我们使用其内置的 ==Sequential== 方法可以自动初始化神经网络需要的参数。

2.torch.nn

2.1torch.nn.Relu和torch.nn.Linear

model = torch.nn.Sequential(torch.nn.Linear(D_in, H),
                            torch.nn.ReLU(),
                            torch.nn.Linear(H, D_out))

pytorch官方中文文档对这段代码的解释是：使用nn包将我们的模型定义为一系列的层.
看完这段描述，我起初以为一个torch.nn对应神经网络中的一层，但是输入层其实什么工作都没干，没有线性激活也没有非线性激活。所以神经网络中的层与torch.nn不是一一对应的，更确切的说，应该是torch.nn与神经网络中的计算模块是一一对应的。

这是一个隐藏层的神经单元（忽略上标和激活函数的错误），对于非线性的神经元其实计算要分为两个部分：线性计算和激活函数非线性计算。完成过吴恩达老师深度学习课后作业的知道，在第一章第三周的作业中，给出的正向传播代码为两部分：线性和非线性。
在了解这之后，就可以知道各torch.nn的作用了（更多的激活函数需要查官方文档）：

1.torch.nn.Linear(D_in, H)：隐藏层的线性激活。
2.torch.nn.ReLU()：隐藏层的非线性激活。
3.torch.nn.Linear(H, D_out)：输出层的线性激活。

这三部分就是整个神经网络前向传播的三个计算步骤。

2.2 神经网络参数的初始化

x = torch.randn(128, 20)  # 输入的维度是（128，20）
m = torch.nn.Linear(20, 30)  # 20,30是指维度

上述代码使用torch.nn.Linear定义了一个简单的线性计算层，注意一下输入的维度：

(n[L-1], n[L]) = (20, 30)

我们查看m的有哪些属性：

我们可以看到m中含有属性weight和bias，weight和bias含有tensor类型的属性data，这就是神经网络每层的权重值和偏移量（根据神经网络的传统定义，每层都要进行线性运算），我们之前用numpy和tensor实现神经网络时，为了方便起见，并未设置偏移量bias。
注意weight的维度，我们传入的维度是（20，30）而初始化weight的维度却是（30，20），我们在前面用numpy和tensor实现的时候，weight的维度都是（n[L-1]，n[L]）。这两种方式与个人编程习惯有关，我个人比较喜欢torch.nn自动初始化weight的方式，因为吴恩达老师深度学习视频中初始化权重weight的维度就是采用（n[L]，n[L-1]）的方式。

3 Sequential

官方文档给出 ==Sequential== 的解释为：nn.Sequential是包含其他模块的模块，并按顺序应用这些模块来产生其输出。

model = torch.nn.Sequential(torch.nn.Linear(D_in, H),
                            torch.nn.ReLU(),
                            torch.nn.Linear(H, D_out))

我们将torch.nn.XXX作为参数传入 ==Sequential== 中，需要注意的是参数的顺序与计算的顺序相关，前向传播的计算顺序是：

1.计算隐藏层线性激活
2.计算隐藏层非线性激活，也就是Relu
3.计算输出层线性激活

看一下Sequential的源代码

def __init__(self, *args):
    super(Sequential, self).__init__()
    if len(args) == 1 and isinstance(args[0], OrdereDict):
        for key, module in args[0].items():
            self.add_module(key, module)
    else:
        for idx, module in enumerate(args):
            self.add_module(str(idx), module)

其实我看的不是太懂，大致干了一件事，把初始化时传入的模块（Linear,Relu）都保存下来。

def forward(self, input):
    for module in self._modules.values():
        input = module(input)
    return input

然后就是Sequential的forward方法，通过for循环依次计算每个计算层的结果，并将结果作为下一个计算层的输入，所以Sequential传入参数时，顺序很重要。
前向传播的代码为：

y_pred = model(x)

所以，输入的x为首个input。

还需要补充一点的是，如果直接用torch.nn.Linear定义的计算层，权重矩阵weight和便宜向量bias的 ==requires_grad== 属性均为False。将其作为参数传入 ==Sequential== 中后，weight和bias的 ==requires_grad== 属性值将变为True。

4.nn中的损失函数

loss_fn = torch.nn.MSELoss(reduction='sum')

这里我们参数设置的是"sum"表示我们计算平方误差的"和"来作为我们的误差值，还有更多的误差计算方法，需要查阅官方文档。
这里我只是定义了损失函数，具体计算得到损失值是下面代码：

loss = loss_fn(y_pred, y)

因为得到的loss依旧是一个tensor类型的值，可以通过backward()方法进行反向传播。

5. 梯度清零

model.zero_grad()

查看zerograd()函数的源代码发现，其利用for循环遍历所有参数，用zero()函数清零。

6. 参数更新

with torch.no_grad():
        for param in model.parameters():
            param -= learning_rate * param.grad

使用tensor为基础的神经网络在进行梯度更新时，几乎都需要使用使用 ==with torch.no_grad():== 。我们在访问神经网络的参数时。使用到了 ==parameters()== 方法，==parameters()== 的返回类型是一个迭代器，可以使用for循环去遍历。每个param是神经网络的一组参数值（tensor变量），在本例中，访问的顺序是w1,b1,w2,b2。

总结

本人也处于学习阶段，可能在某些知识点上的理解有问题，欢迎指正。另外，有些知识点我并没有深入的了解，比如上文中提到的损失函数，但是这些知识点特别重要，我在后续的学习中肯定会去进一步了解，到时候再把相应的知识补上。

前言