一、SVM（support vector machines）

支持向量机（support vector machines，SVM）是一种二分类模型，它将实例的特征向量映射为空间中的一些点，SVM 的目的就是想要画出一条线，以 “最好地” 区分这两类点，以至如果以后有了新的点，这条线也能做出很好的分类。

注意SVM是一个二分类模型，理论上来说是不支持多分类的，但是通过一些方法和处理也可以用SVM完成多分类的任务，具体的方法在后文中会给出。为了更加直观地理解算法，还是以二维数据为例进行解释。

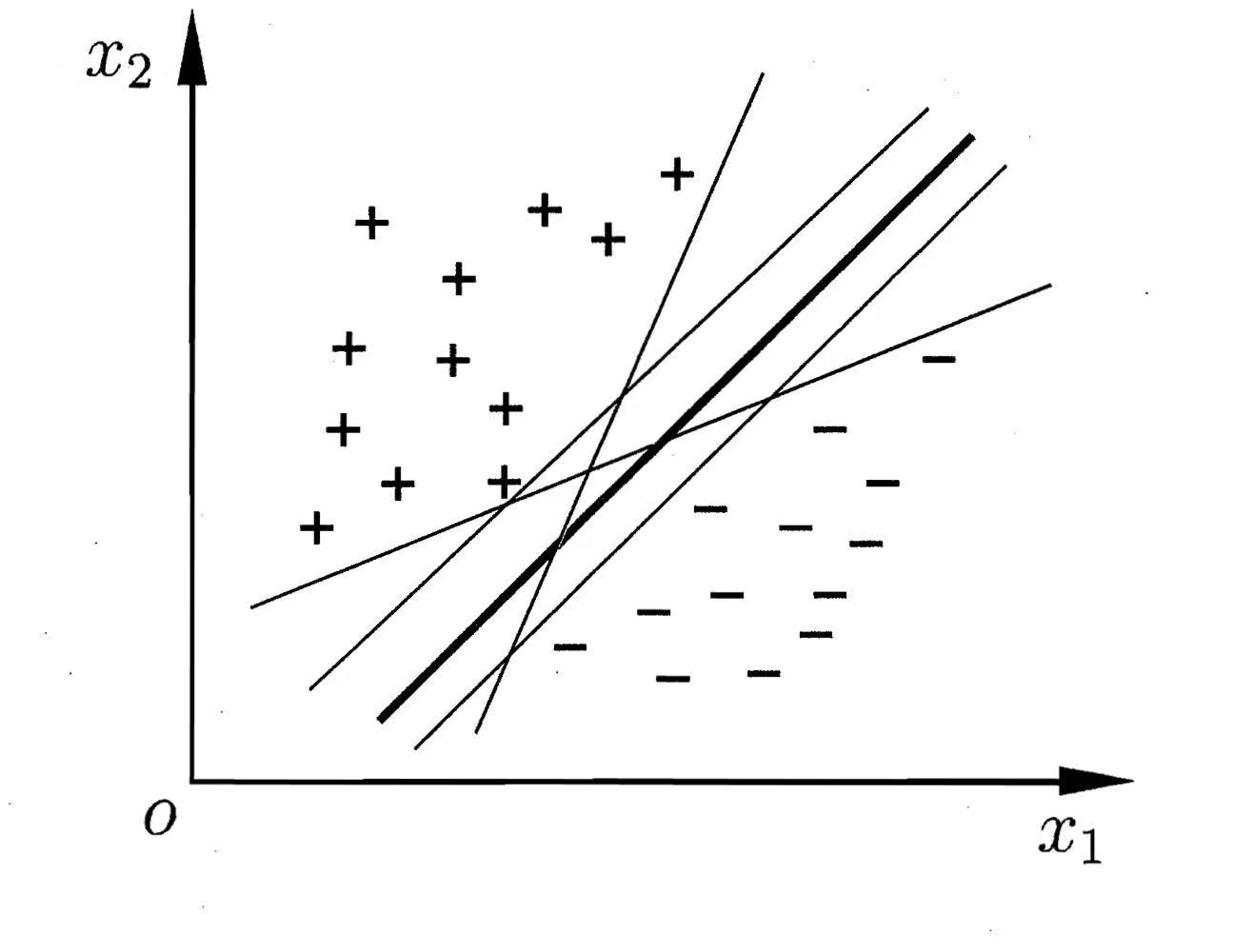
上图中的 + 和 - 表示两类标签的样本点，想要把这两类样本点划分开其实有很多种方案，图中的每条直线表示不同的方案，每个方案也确实都能将两类样本点完全划分开来，但是直观上看，加粗的那条直线表现效果是最好的，因为该直线位于两类样本点的“正中间”。支持向量机的目的就是为了找到最优的那条直线，对于新的数据，通过计算它位于直线的哪一侧来进行分类。

为什么处于两类样本“正中间”的直线是最优的方案？因为我们只是在训练集上进行划分，倘若划分得到的直线离两类样本点都特别近，那么对于新的样本点出错的可能性就越大，鲁棒性较差。

以上就是支持向量机对二维数据分类的核心思想，对于高维数据也类似，支持向量机旨在找到一个最优的划分超平面，在二维数据中。这个超平面就是一条直线。

还是以二维数据为例，现在我们知道支持向量机的目的是找到“正中间”的那条直线，如何定量地去衡量这个所谓的“正中间”，这就要引入“支持向量”和“间隔”地概念。

在二维空间中，超平面（也就是直线）的线性方程可以描述为：
$$
\omega^Tx+b=0(\omega为法向量)\
$$
在二分类任务中，当确定了可以正确分类的超平面时，对于样本(xi,yi)，满足如下关系式：
$$
y_i=+1,\omega^Tx_i+b>0\\
y_i=-1,\omega^Tx_i+b<0
$$

那什么是支持向量呢？我们使分类的标准更加严格一些，单纯的通过正负判断可能会使得超平面鲁棒性不高：
$$
\omega^Tx_i+b\geq+1，y_i=+1\\
\omega^Tx_i+b\leq-1，y_i=-1\
$$

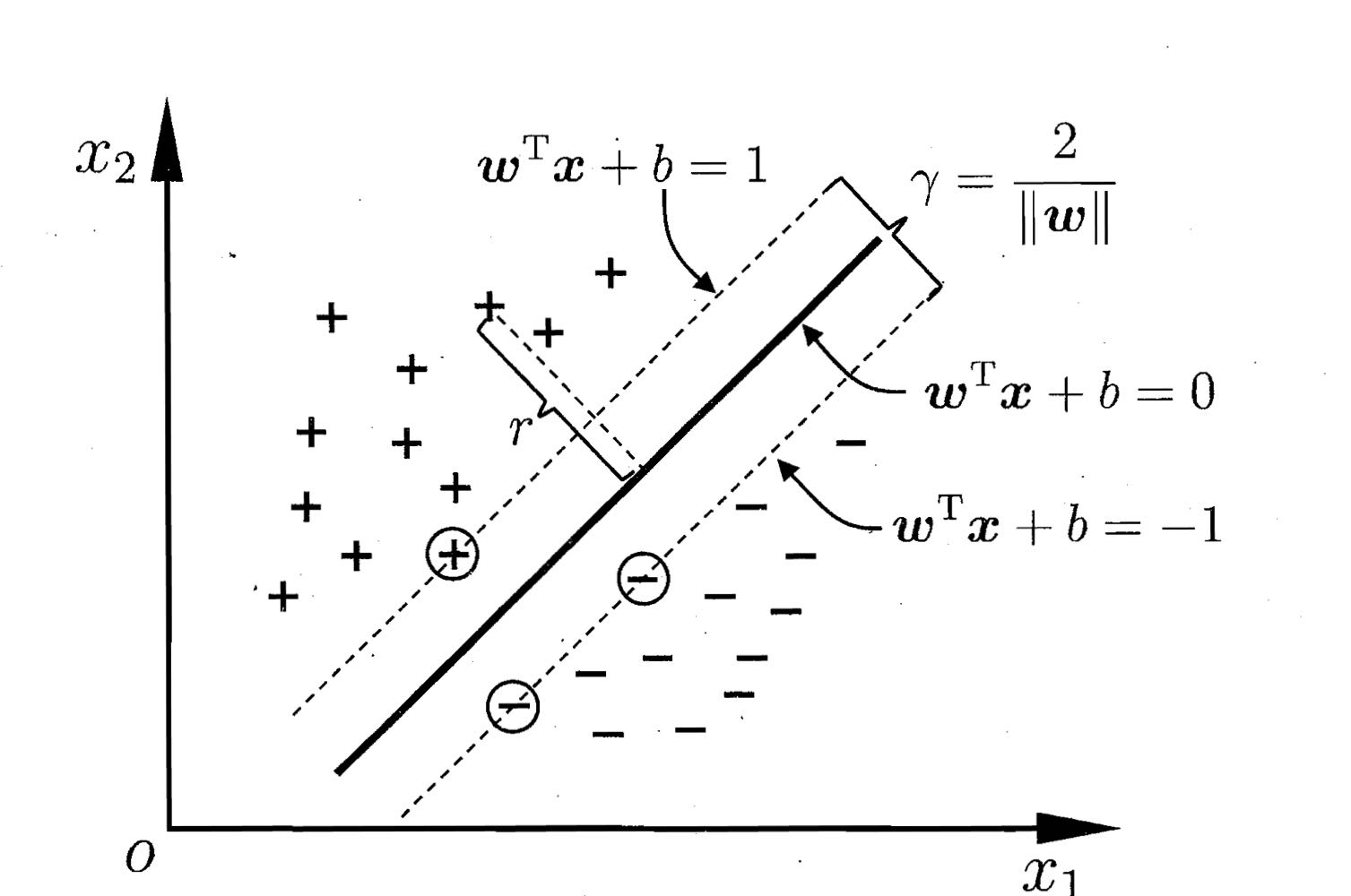
而我们只关注使等号成立的样本点，这些样本点被称为“支持向量”，从下图可以看出，虚线上的点到划分超平面的距离都是一样的，实际上只有这几个点共同确定了超平面的位置。

两个异类支持向量到超平面之间的距离之和被称为“间隔”，实际上就是图中两虚线之间的距离：
$$
\gamma=\frac{2}{||\omega||}\
$$
而支持向量机的目标是最大化这个间隔，求得最大间隔时的w和b，以此来确定超平面的位置:
$$
\underset{\omega,b}{max}\frac{2}{||\omega||}\\
s.t.y_i(\omega^Tx_i+b)\geq1
$$
上述最大化问题可以转化为下面最小化问题：
$$
\underset{\omega,b}{min}\frac{1}{2}||\omega||^2\\
s.t.y_i(\omega^Tx_i+b)\geq1
$$

二、SVM最优化求解

SVM怎样求解得到参数w和b，涉及到一些公式推导，本人也还在学习中，这里就给出大致的流程，其中的原理就不给出分析。主要思路是用拉格朗日乘子法得到原问题的对偶问题，再进行求解。

首先是将原先的最小化问题根据约束条件，转化为拉格朗日函数：
$$
L(\omega,b,\alpha)=\frac{1}{2}||\omega||^2+\sum_{i=1}^m\alpha_i(1-y_i(\omega^Tx_i+b))(1),\alpha_i\geq0
$$
原始问题就变为：
$$
\underset{\omega,b}{min}(\underset{\alpha_i\geq0}{max}L(\omega,b,\alpha))
$$
其对偶问题为：
$$
\underset{\alphai\geq0}{max}(\underset{\omega,b}{min}L(\omega,b,\alpha))
$$
令L对ω和b的偏导为零可得：
$$
\omega = \sum{i=1}^{m}\alpha_iy_ixi(2)\\
0=\sum{i=1}^m\alpha_iyi(3)
$$
将公式(2)和(3)带入到公式(1)中，就可得到原问题的对偶问题表达式：
$$
\underset{\alpha}{max}\sum{i=1}^{m}\alphai-\frac{1}{2}\sum{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_jx_j^Txj(4)\\
s.t.\sum{i=1}^{m}\alpha_iy_i=0,\alphai\geq0
$$
解出α后就可得到ω和b的模型：
$$
f(x)=\omega^Tx+b=\sum{i=1}^{m}\alpha_iy_ix_ix+b(5)
$$
怎么求解公式(4)就需要用到SMO算法，SMO算法将在下一篇博客中介绍。对于新的样本点，将其带入到公式(6)中，根据结果的正负来对样本进行分类。进一步研究公式发现，参与运算的训练样本只需支持向量，也就是说最终模型只与支持向量有关。

三、核函数

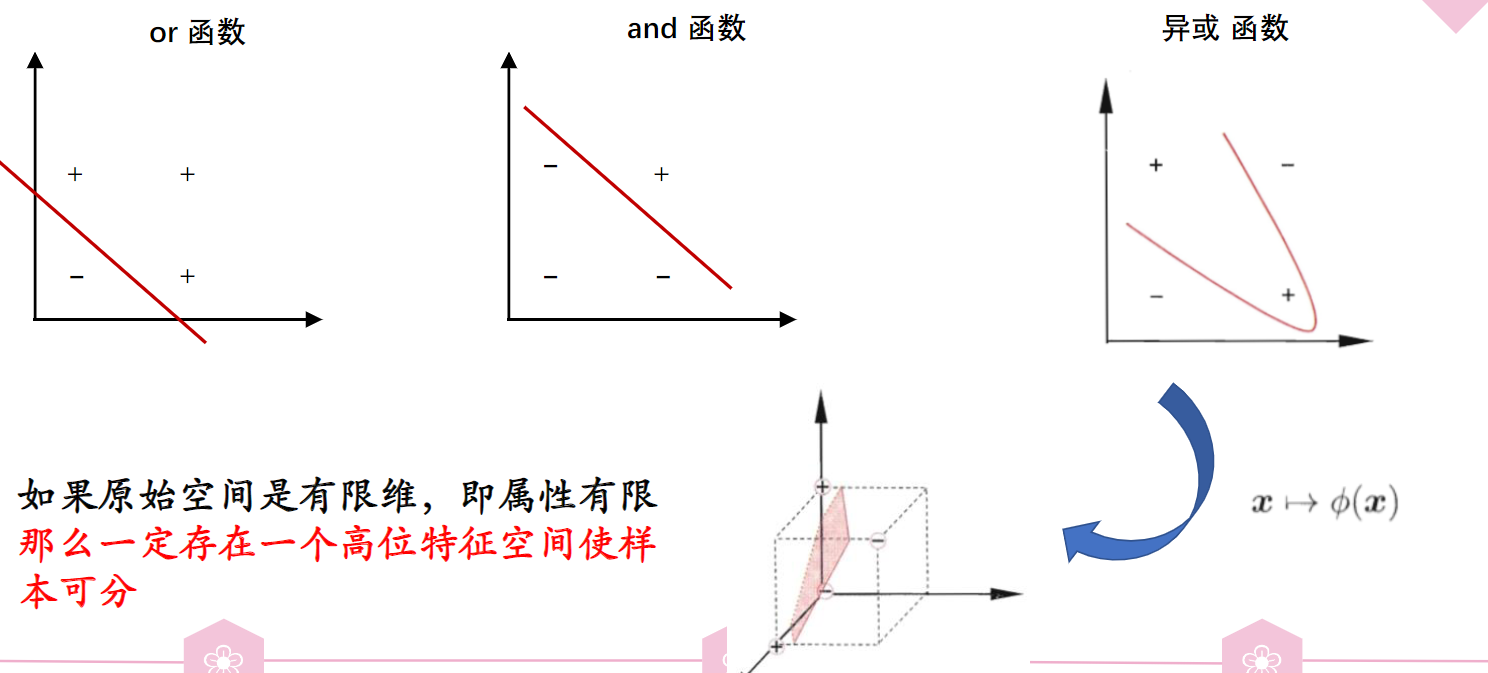
在处理实际问题的过程中，我们难免会遇到这样一个问题：训练样本在原始样本空间内线性不可分，也就是找不到一个能正确划分两类样本的超平面，最典型的就是异或问题：

对于这样的情况，可以将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。如果原始空间是有限维，那么一定存在一个高维特征空间使样本可分。

令Φ(x)表示x映射后的特征向量，则特征空间中的超平面可表示为：
$$
f(x)=w^T\phi(x)+b
$$
对偶问题的表达式为：
$$
\underset{\alpha}{max}\sum_{i=1}^{m}\alphai-\frac{1}{2}\sum{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\phi(x_i)^T\phi(xj)\\
s.t.\sum{i=1}^{m}\alpha_iy_i=0,\alpha_i\geq0
$$
这样处理起来貌似和之前的处理没多大区别，但是存在这样一个问题，那就是特征空间的维数可能很高，这就使得直接计算Φ(xi)TΦ(xj)比较困难，这时我们想在原始空间中找到这样一个函数，其运算结果等于Φ(xi)TΦ(xj)，这就是核函数：
$$
\kappa(x_i,x_j)=<\phi(x_i),\phi(j)>=\phi(x_i)^T\phi(xj)
$$
这样就可以在原始低维空间内计算κ函数即可得到xi与xj在高维空间的内积结果，对偶函数就变为：
$$
\underset{\alpha}{max}\sum{i=1}^{m}\alphai-\frac{1}{2}\sum{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\kappa(x_i,xj)\\
s.t.\sum{i=1}^{m}\alpha_iy_i=0,\alphai\geq0
$$
求解后得到模型：
$$
f(x)=\sum{i=1}^m\alpha_iy_i\kappa(x,x_i)+b
$$
怎样设计和确定核函数呢？只要一个对称函数所对应的核矩阵半正定，它就能作为核函数使用。这句话什么意思，博主并不清楚，但是存在一些常用的核函数，可以都尝试一下。

四、硬间隔和软间隔

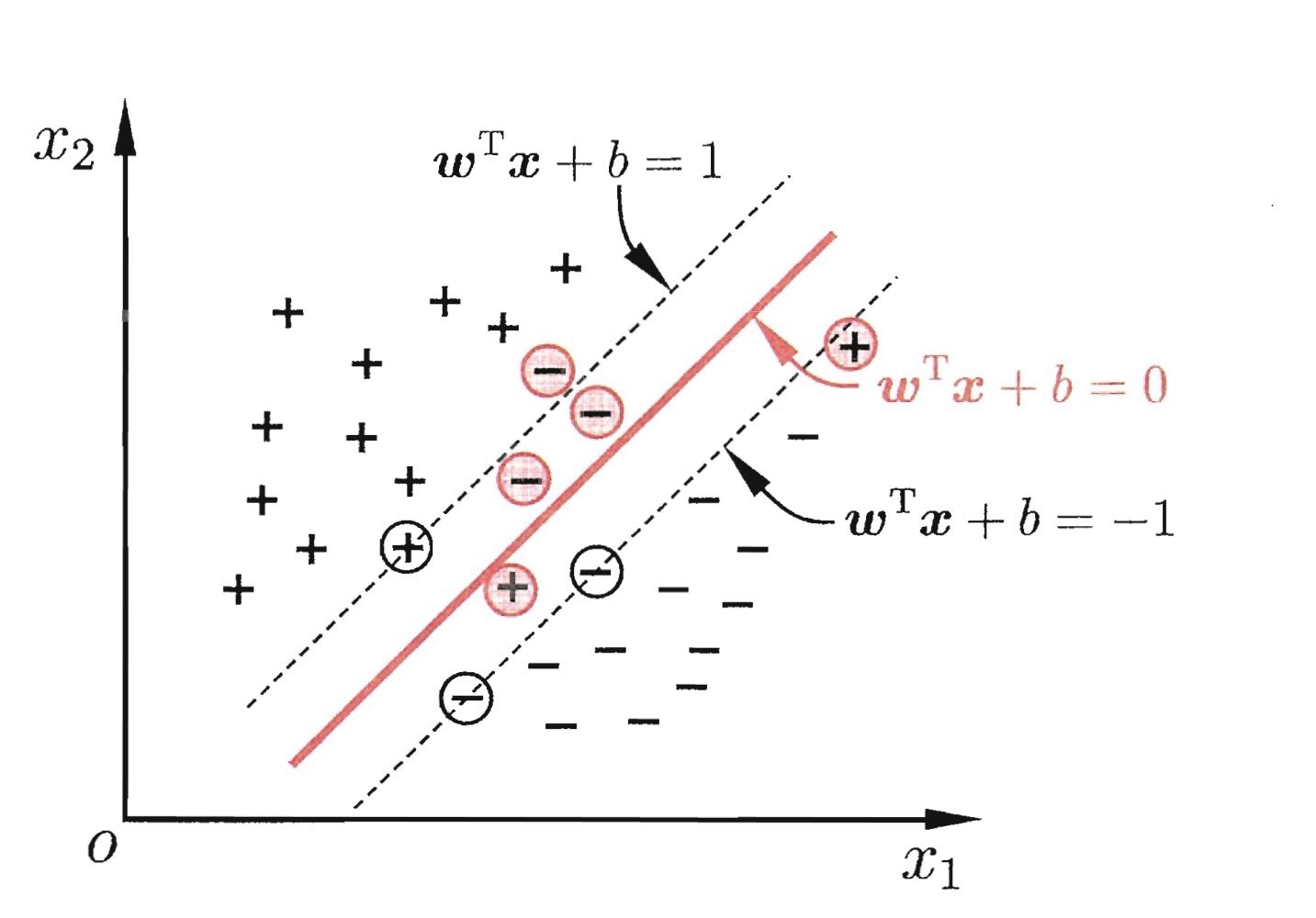
上文中我们默认在最大化间隔的同时，间隔中间不允许存在样本点，这被称为“硬间隔”，但是实际情况往往是无法找到不存在没有样本点的最大间隔，我们允许间隔中间存在一些样本点，这被称为“软间隔”，即存在某些样本不满足下面的约束条件：
$$
y_i(\omega^Txi+b)\geq1
$$
这时优化目标可写为：
$$
\underset{\omega,b}{min}\frac{1}{2}||\omega||^2+C\sum{i=1}^m\zeta_{0/1}(y_i(\omega^Tx_i+b)-1)
$$

其中C为常数，我们称之为“惩罚因子”，ζ为损失函数，上式中的是“0/1损失函数”：

$$
\zeta_{0/1}(z)=\left\{
\begin{matrix}
1,if z<0\\
0,otherwise
\end{matrix}
\right.
$$

当然也存在其他损失函数，比如：

$$
hinge损失：\zeta{hinge}(z)=max(0,1-z)\\
指数损失：\zeta{exp}(z)=exp(-z)\\
对率损失：\zeta_{log}(z)=log(1+exp(-z))
$$
我们一般会引入“松弛变量”来将优化目标的式子进行重写：
$$
\underset{\omega,b,\xii}{min}\frac{1}{2}||\omega||^2+C\sum{i=1}^{m}\xii
$$
理解了软间隔的具体概念和公式后，接下来看看软间隔下的对偶问题和约束条件，首先是拉格朗日函数：
$$
L(\omega,b,\alpha,\xi,\mu)=\frac{1}{2}||\omega||^2+C\sum{i=1}^m\xii+\sum{i=1}^{m}\alpha_i(1-\xi_i-y_i(\omega^Txi+b))-\sum{i=1}^{m}\mu_i\xi_i\
(其中\alpha_i\geq0,\xii\geq0,均为拉格朗日乘子)
$$
其对偶问题的表达式为：
$$
\underset{\alpha}{max}\sum{i=1}^m\alphai-\frac{1}{2}\sum{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_jx_i^Txj\\
s.t.\sum{i=1}^m\alpha_iy_i=0,0\leq\alpha_i\leq C
$$
软间隔支持向量机的KKT约束条件为：
$$
\left\{
\begin{matrix}
\alpha_i\geq0,\mu_i\geq0,\\
y_if(x_i)-1+\xi_i\geq0,\\
\alpha_i(y_if(xi)-1+\xi_i)=0,\\
\xi_i\geq0,\mu_i\xi_i=0
\end{matrix}
\right.
$$
关于具体的公式推导感兴趣的同学可以去查查相关资料，博主还在学习中，若以后有时间会来更新这一部分的公式推导内容。

五、SVM解决多分类问题

支持向量机实现多分类的主要途径有三种：（1）直接法，直接在目标函数上进行修改，将多个分类面的参数求解合并到一个最优化问题中，通过求解该最优化问题“一次性”实现多类分类。这种方法看似简单，但其计算复杂度比较高，实现起来比较困难，只适合用于小型问题中；（2）间接法，主要是通过组合多个二分类器来实现多分类器的构造；（3）层次分类法首先将所有类别分成两个子类，再将子类进一步划分成两个次级子类，如此循环，直到得到一个单独的类别为止。具体可以参考博客：

[SVM实现多分类的三种方案](https://www.cnblogs.com/CheeseZH/p/5265959.html)

可能第二种方法最好实现也最容易理解，以三分类为例，样本标签为[1,2,3]，我们需要训练三个支持向量机。第一个SVM需要把所有标签为1的样本标记为正例，把标签为2和3的样本标记为负例。同理，第二个SVM需要把所有标签为2的样本标记为正例，把标签为1和3的样本标记为负例，第三个SVM需要把所有标签为3的样本标记为正例，把标签为1和2的样本标记为负例。这三个SVM分开训练，对于新样本，选取结果最大的分类器作为样本的对应分类。

这需要注意一个问题，就是正例样本和负例样本极度不平衡，对分类器的影响可能比较大，需要对数据进行筛选。