声明

  本博客只是记录一下本人在深度学习过程中的学习笔记和编程经验，大部分代码是参考了【中文】【吴恩达课后编程作业】Course 2 - 改善深层神经网络 - 第二周作业这篇博客，对其代码实现了复现，代码或文字表述中还存在一些问题，请见谅，之前的博客也是主要参考这个大佬。下文中的完整代码已经上传到百度网盘中，提取码：af12。

一、任务描述

  这次作业我们的主要任务是以下四个：

1.划分mini-batch训练集。
2.基于mini-batch，使用常规的梯度下降法。
3.基于mini-batch，使用momentum梯度下降法。
4.基于mini-batch，使用Adam优化算法。

  这次作业的主要目的不是在于神经网络的搭建，关于神经网络的前向传播和反向传播的具体实现不再进行过多赘述，完整代码已经上传到百度网盘中。

二、编程实现

1.使用的数据

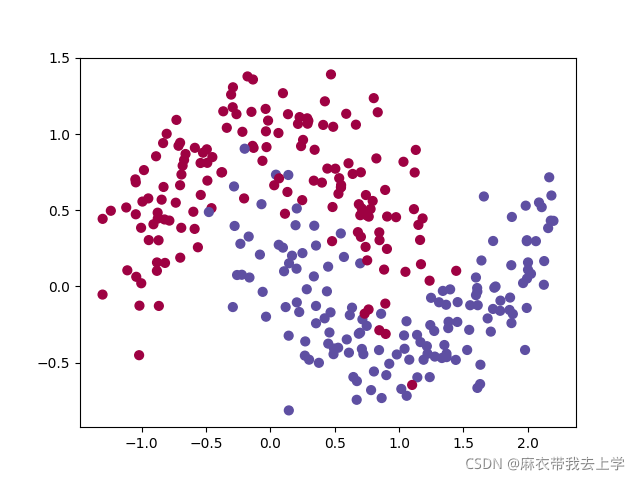
  这次作业使用的数据是使用sklearn库生成的，用matplotlib绘制如下：

  生成数据的代码为：

def load_dataset(is_plot=True):
    """
    加载数据
    :param is_plot: 是否绘制数据散点图
    :return: train_X -(2,300)
             train_Y -(1,300)
    """
    np.random.seed(3)
    train_X, train_Y = sklearn.datasets.make_moons(n_samples=300, noise=.2)  # 300 #0.2
    # Visualize the data
    if is_plot:
        plt.scatter(train_X[:, 0], train_X[:, 1], c=train_Y, s=40, cmap=plt.cm.Spectral)
        plt.show()
    train_X = train_X.T
    train_Y = train_Y.reshape((1, train_Y.shape[0]))

    return train_X, train_Y

  从绘制的散点图可以看出，这次需要解决的问题是一个二分类任务。train_X的维度为(2,300)，train_Y的维度为(1,300)。

2.mini-batch处理数据集

  训练集一共300条数据，我们需要根据mini_batch_size的值来进行划分，使得每个batch的训练数据的数量为mini_batch_size。需要注意的是，我们希望每一个epoch所划分的结果都互不相同，所以在划分之前我们需要随机打乱训练集，这里用到的是numpy中的 ==permutation== 函数，他会根据传入的参数m生成一个包含0至（m-1）所有数的随机打乱的序列。另外这里还用到了 ==math.floor== 函数，它的作用是向下取整。

def random_mini_batches(X, Y, mini_batch_size=64, seed=0):
    """
    随机打乱训练集，并创建一个随机的mini_batch列表
    :param X: 训练集
    :param Y: 训练集标签
    :param mini_batch_size:每一个mini_batch的样本数量
    :param seed: 随机种子
    :return:
    """
    np.random.seed(seed)
    m = X.shape[1]
    mini_batches = []

    permutation = list(np.random.permutation(m))
    shuffled_X = X[:, permutation]
    shuffled_Y = Y[:, permutation].reshape(1, m)

    nums = math.floor(m / mini_batch_size)
    for i in range(0, nums):
        mini_batch_X = shuffled_X[:, i * mini_batch_size:(i + 1) * mini_batch_size]
        mini_batch_Y = shuffled_Y[:, i * mini_batch_size: (i + 1) * mini_batch_size]

        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
    if m % mini_batch_size != 0:
        # 获取最后剩余的部分
        mini_batch_X = shuffled_X[:, mini_batch_size * nums:]
        mini_batch_Y = shuffled_Y[:, mini_batch_size * nums:]

        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
    return mini_batches
   ```
## 3.mini-batch梯度下降法
  从编程角度来看，基于mini-batch的梯度下降法和普通的梯度下降法差别并不是很大，前向传播，反向传播，参数更新和计算损失的函数基本不变。
  我们的数据总量是300条，当设置mini-batch-size大小为64时，我们可以得到5个mini-batch，普通的梯度下降法是一次性处理这300条数据，然后循环num_iterations（迭代的次数）次，每次循环更新神经网络的参数。
  而min-batch的梯度下降法一次处理64条数据（最后一个batch可能不足64条），处理完一个batch后直接进行神经网络梯度更新，模型并未见到所有的数据就发生了参数更新。因此，mini-batch梯度下降法涉及到两层循环，最外层循环还是迭代次数（在mini-batch中更喜欢称为epoch），内层循环则需要遍历所有的mini-batch（这里是5个）。这里给出部分代码：

```python
 for i in range(num_epochs):
        seed = seed + 1
        mini_batches = opt_utils.random_mini_batches(X, Y, mini_batch_size, seed)

        for mini_batch in mini_batches:
            (mini_batch_X, mini_batch_Y) = mini_batch
            A3, cache = opt_utils.forward_propagation(mini_batch_X, parameters)
            cost = opt_utils.compute_cost(A3, mini_batch_Y)
            grads = opt_utils.backward_propagation(mini_batch_X, mini_batch_Y, cache)
            if optimizer == "gd":
                parameters = opt_utils.update_parameters_with_gd(parameters, grads, learning_rate)

4.momentum梯度下降方法

  momentum梯度下降法的原理其实并不复杂，关于编程实现需要注意以下几点：

1.需要超参数β
2.需要初始化v用来记录公式中的v(dW)和v(db)，v(dW)的维度应该与W相同，v(db)的维度应该与b相同。
3.更新神经网络参数时需要计算v(dW)和v(db)的值，计算公式中的第一项β*v(dW)中的v(dW)是上一次迭代计算的结果。

  参数初始化：

def initialize_momentum_v(parameters):
    """
    用神经网络中的参数初始化动量梯度下降需要的参数:Vb和Vw
    :param parameters: 神经网络中的参数W和b
    :return: v -字典变量：- keys: "dW1", "db1", ..., "dWL", "dbL"
                        - values:与相应的梯度/参数维度相同的值为零的矩阵。
    """
    L = len(parameters) // 2
    v = {}

    for l in range(0, L):
        v["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])
        v["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])

    return v

  更新参数：

def update_parameters_momentum(parameters, v, grads, beta, learning_rate):
    """
    在梯度下降完成后，更新神经网络参数参数
    :param parameters: 神经网络的参数：W和b
    :param v: momentum保存的变量
    :param grads: 反向传播计算的梯度
    :param beta: momentum更新的参数
    :param learning_rate: 学习率
    :return:
    """
    L = len(parameters) // 2

    for l in range(0, L):
        v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] + (1 - beta) * grads["dW" + str(l + 1)]
        v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * grads["db" + str(l + 1)]
        # 更新神经网络参数
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * v["dW" + str(l + 1)]
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * v["db" + str(l + 1)]
    return parameters, v

  参数初始化和更新参数的函数都保存在 ==momentum.py== 文件中。

5.Adam优化算法

  Adam优化算法其实是momentum和RMSprop的一个结合，编程注意事项：

1.需要超参数β1，β2和防除零参数
2.初始化每层v和s需要与当前层的W和b的维度相同
3.需要进行偏差修正

  参数初始化：

def initialize_adam_sv(parameters):
    """
    初始化Adam优化算法需要的参数：v和s
    :param parameters: 神经网络的参数
    :return: v和s -字典变量：- keys: "dW1", "db1", ..., "dWL", "dbL"
                           - values:与相应的梯度/参数维度相同的值为零的矩阵。
    """
    L = len(parameters) // 2
    s = {}
    v = {}

    for l in range(0, L):
        s["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])
        s["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])

        v["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])
        v["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])

    return v, s

  更新参数：

def update_parameters_with_adam(parameters, grads, v, s, t, beta1, beta2, epsilon, learning_rate):
    """
    使用Adam优化算法更新神经网络参数
    :param parameters: 神经网络参数
    :param grads: 反向传播求得的梯度
    :param v:Adam的变量，第一个梯度的移动平均值，是一个字典类型的变量
    :param s:Adam的变量，平方梯度的移动平均值，是一个字典类型的变量
    :param t:当前迭代的次数
    :param beta1:momentum的一个超参数
    :param beta2:RMSprop的一个超参数
    :param epsilon:防止除零添加的参数
    :param learning_rate:学习率
    :return:
    """
    L = len(parameters) // 2
    v_correct = {}
    s_correct = {}

    for l in range(L):
        v["dW" + str(l + 1)] = beta1 * v["dW" + str(l + 1)] + (1 - beta1) * grads["dW" + str(l + 1)]
        v["db" + str(l + 1)] = beta1 * v["db" + str(l + 1)] + (1 - beta1) * grads["db" + str(l + 1)]

        s["dW" + str(l + 1)] = beta2 * s["dW" + str(l + 1)] + (1 - beta2) * np.square(grads["dW" + str(l + 1)])
        s["db" + str(l + 1)] = beta2 * s["db" + str(l + 1)] + (1 - beta2) * np.square(grads["db" + str(l + 1)])

        # 偏差修正
        v_correct["dW" + str(l + 1)] = v["dW" + str(l + 1)] / (1 - np.power(beta1, t))
        v_correct["db" + str(l + 1)] = v["db" + str(l + 1)] / (1 - np.power(beta1, t))

        s_correct["dW" + str(l + 1)] = s["dW" + str(l + 1)] / (1 - np.power(beta2, t))
        s_correct["db" + str(l + 1)] = s["db" + str(l + 1)] / (1 - np.power(beta2, t))

        # 参数更新
        temp = s_correct["db" + str(l + 1)] + epsilon
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * (v_correct["dW" + str(l + 1)] / (np.sqrt(s_correct["dW" + str(l + 1)] + epsilon)))
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * (
                    v_correct["db" + str(l + 1)] / (np.sqrt(s_correct["db" + str(l + 1)] + epsilon)))

    return parameters, v, s

  参数初始化和更新参数的函数都保存在 ==adam_gd.py== 文件中。

6.主控模型

def model(X, Y, layers_dims, optimizer, learning_rate=0.0007, mini_batch_size=64, beta=0, beta1=0.9, beta2=0.999,
          epsilon=1e-8, num_epochs=10000, print_cost=True, is_plot=True):
    """
    主控模型
    :param X: 输入数据
    :param Y: 输入数据的标签集
    :param layers_dims: 各层神经元的个数(列表)
    :param optimizer: 优化类型
    :param learning_rate: 学习率
    :param mini_batch_size: 批处理数量大小
    :param beta: 动量优化的参数
    :param beta1: 用于计算梯度后的指数衰减的估计的超参数
    :param beta2: 计算平方梯度后的指数衰减的估计的超参数
    :param epsilon: 避免除0的超参数
    :param num_epochs:迭代轮数
    :param print_cost:是否打印误差值
    :param is_plot:是否绘制误差曲线
    :return:
    """

    L = len(layers_dims)
    costs = []
    epoch_count = 0
    seed = 10

    # 初始化神经网络参数
    parameters = opt_utils.initialize_parameters(layers_dims)

    # 选择优化算法
    if optimizer == "gd":
        pass
    elif optimizer == "momentum":
        v = momentum_gd.initialize_momentum_v(parameters)
    elif optimizer == "adam":
        v, s = adam_gd.initialize_adam_sv(parameters)
    else:
        print("optimizer参数错误")

    # 开始学习
    for i in range(num_epochs):
        seed = seed + 1
        mini_batches = opt_utils.random_mini_batches(X, Y, mini_batch_size, seed)

        for mini_batch in mini_batches:
            (mini_batch_X, mini_batch_Y) = mini_batch
            A3, cache = opt_utils.forward_propagation(mini_batch_X, parameters)
            cost = opt_utils.compute_cost(A3, mini_batch_Y)
            grads = opt_utils.backward_propagation(mini_batch_X, mini_batch_Y, cache)
            if optimizer == "gd":
                parameters = opt_utils.update_parameters_with_gd(parameters, grads, learning_rate)
            elif optimizer == "momentum":
                parameters, v = momentum_gd.update_parameters_momentum(parameters, v, grads, beta, learning_rate)
            elif optimizer == "adam":
                epoch_count = epoch_count + 1
                parameters, v, s = adam_gd.update_parameters_with_adam(parameters, grads, v, s, epoch_count, beta1, beta2,
                                                                 epsilon, learning_rate)
            else:
                print("optimizer参数错误")
        if i % 100 == 0:
            costs.append(cost)
            # 是否打印误差值
            if print_cost and i % 1000 == 0:
                print("第" + str(i) + "次遍历整个数据集，当前误差值：" + str(cost))
    if is_plot:
        plt.plot(costs)
        plt.ylabel('cost')
        plt.xlabel('epochs (per 100)')
        plt.title("Learning rate = " + str(learning_rate))
        plt.show()
    return parameters

7.测试结果

  测试代码如下，神经网络结构为3层，通过改变optimizer参数的值可以选取不同的优化算法。

if __name__ == "__main__":
    layers_dims = [train_X.shape[0], 5, 2, 1]
    parameters = model(train_X, train_Y, layers_dims, optimizer="adam", is_plot=True)
    # 预测
    preditions = opt_utils.predict(train_X, train_Y, parameters)

    # 绘制分类图
    plt.title("Model with Gradient Descent optimization")
    axes = plt.gca()
    axes.set_xlim([-1.5, 2.5])
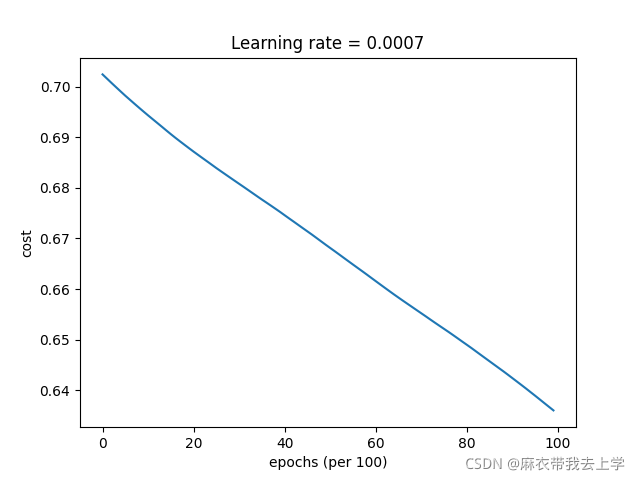
    axes.set_ylim([-1, 1.5])

7.1 未使用mini-batch的梯度下降法

  损失曲线：

  决策边界：

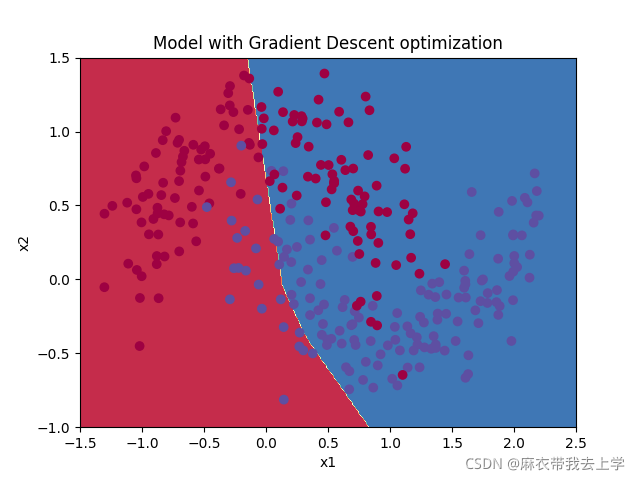
  在训练集上的准确率：

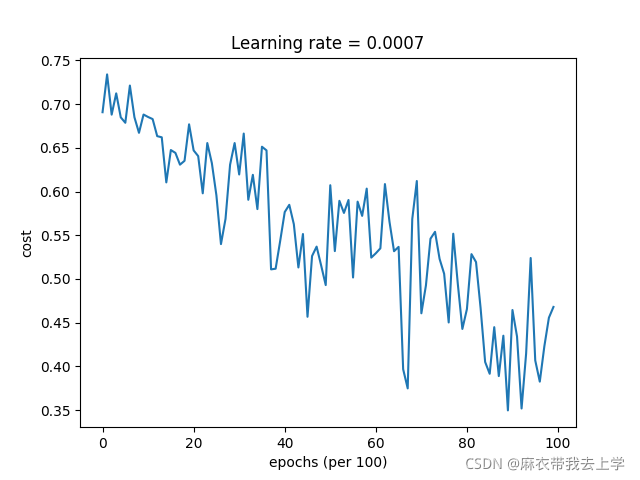
7.2 使用mini-batch的梯度下降法

  损失曲线：

  决策边界：

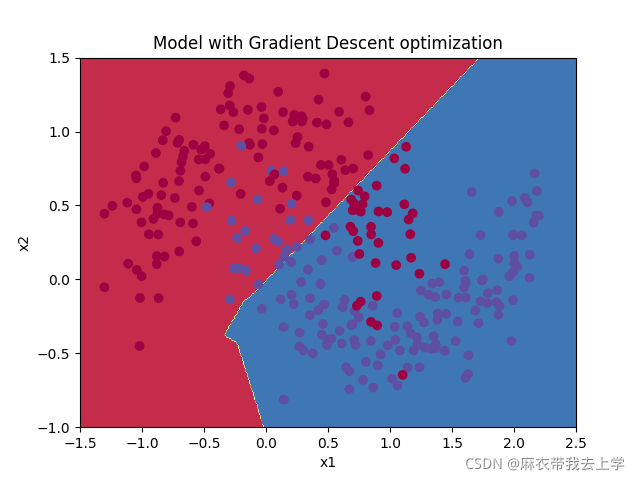
  在訓練集上的準確率：

  可以看出，使用mini-batch后準確率有所提高，损失曲线也如视频中那样震荡，但是大体呈下降趋势。

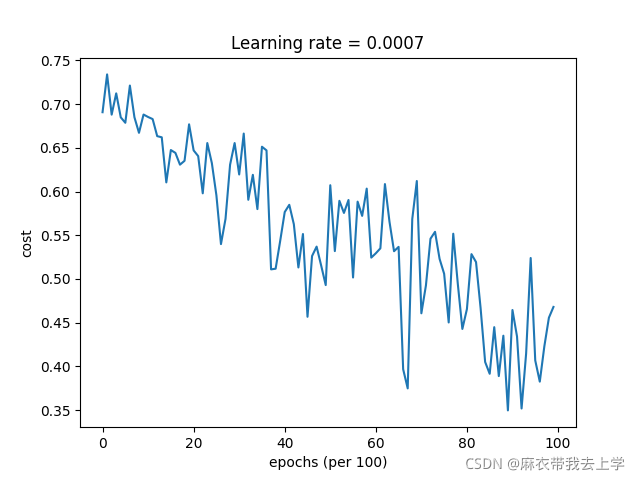
7.3momentum梯度下降法

  损失曲线：

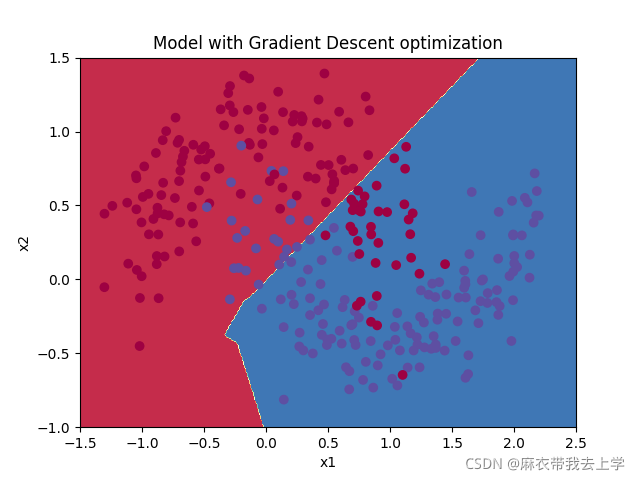
  决策边界：

  在训练集上的准确率：

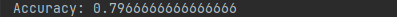
  可以看出准确率并没有提升。

7.4 Adam优化算法

  损失曲线：

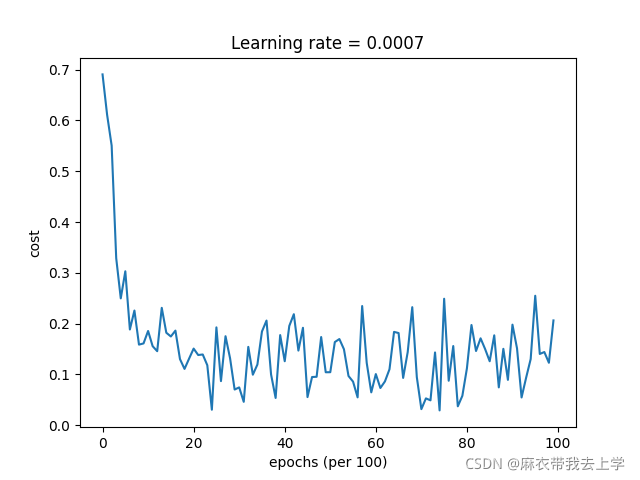
  决策边界：

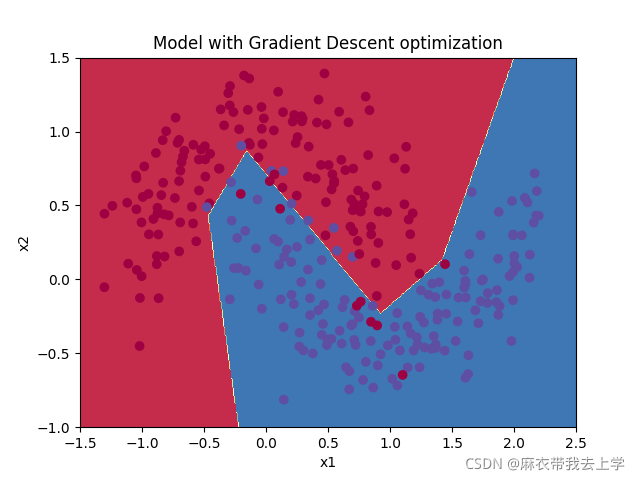
  在训练集上的准确率：

  可以看出，使用Adam优化算法不仅损失函数曲线下降的更快，准确率也有明显提高。

总结

  通过对比实验，可以看出Adam优化算法的性能还是挺高的，本文只进行了基于mini-batch的优化算法，可以将Adam优化算法用于普通的梯度下降法中，也可以优化模型，提高准确率。