POSSUM 网站一共给出了21种PSSM的”变形“,这21种”变形“出自13篇不同的论文,我简单阅读这13篇论文,对各个PSSM做了一个简单的归纳,为了与原始论文中的描述一致,下面描述中采用的PSSM的维数为(蛋白质长度,20),与维基百科正好相反。
一、21种”变形“PSSM
POSSUM的原论文:
Wang J, Yang B et al. POSSUM: a bioinformatics toolkit for generating numerical sequence feature descriptors based on PSSM profiles. Bioinformatics 2017;33(17):2756-2758. DOI: 10.1093/bioinformatics/btx302.
给出了21种生成PSSM的一个概括:
| Descriptors groups | Descriptor | Number |
|---|---|---|
| Row transformations | ACC-PSSM | 20 |
| D-FPSSM | 20 | |
| smoothed-PSSM | * | |
| AB-PSSM | 400 | |
| PSSM-composition | 400 | |
| RPM-PSSM | 400 | |
| S-FPSSM | 400 | |
| Column transformations | DPC-PSSM | 400 |
| k-separated-bigrams-PSSM | 400 | |
| tri-gram-PSSM | 8000 | |
| EEDP | 400 | |
| TPC | 400 | |
| Mixture of row and column transformations | EDP | 20 |
| RPSSM | 110 | |
| Pse-PSSM | 40 | |
| DP-PSSM | * | |
| PSSM-AC | * | |
| PSSM-CC | * | |
| Combination of above descriptors | AADP-PSSM | 420 |
| AATP | 420 | |
| MEDP | 420 |
上表中*表示的是结果受参数影响,POSSUM网站提供了设置这些参数的接口。
二、AAC-PSSM/DPC-PSSM/AADP-PSSM
Liu, T., Zheng, X. and Wang, J. (2010) Prediction of protein structural class for low-similarity sequences using support vector machine and PSI-BLAST profile, Biochimie, 92, 1330-1334.
原论文中,对得到的原始PSSM运用sigmoid函数将矩阵中的值映射到0-1之间,再进行接下来的操作,通过sigmoid函数并未改变矩阵的形状。
AAC-PSSM的计算公式为:
$$
X=(x_1,x_2,x3,..,x{20})^T\\
xj=\frac{1}{L}\sum{i=1}^{L}p_{i,j}\\
(j=1,2,3,...,20;L为蛋白质序列的长度)
$$
通过公式可知,ACC-PSSM就是在将PSSM进行sigmoid操作后,对其每列求平均值,最后可以将一条蛋白质序列嵌入成一个20维的向量。
DPC-PSSM的计算公式为:
$$
Y=(y{1,1},...,y{1,20},...,y{2,1},...,y{2,20},...,y{20,1},...,y{20,20})^T\\
y{i,j} = \frac{1}{L-1}\sum{k=1}^{L-1}p{k,i} \times p{k+1,j},(1\leq i,j\leq20)
$$
通过公式可知,DPC-PSSM就是将相邻两行的第i个氨基酸和第j氨基酸乘积求和并取平均,最后可以将一条蛋白质序列嵌入成400维向量。
AADP-PSSM 就是将上述两种PSSM进行拼接得到一个420维的向量,作为蛋白质序列的嵌入。
三、D-FPSSM/S-FPSSM
Zahiri, J., et al. (2013) PPIevo: protein-protein interaction prediction from PSSM based evolutionary information, Genomics, 102, 237-242.
首先根据原始PSSM得到FPSSM,FPSSM是在PSSM的基础上过滤掉矩阵中的负值,因此FPSSM和PSSM的形状是一致的。
D-FPSSM 的计算公式为:
$$
D=(d_1,d2,...,d{20})\\
dj=\sum{i=1}^{L}fp_{i,j}\\
d_j=\frac{d_j-min}{max \times L}
$$
根据公式可知,D-FPSSM是将FPSSM的每一行求和后减去对应行的最小值,并除以该行的最大值和序列长度的乘积。D-FPSSM可以将蛋白质嵌入成一个20维的向量。
S-FPSSM 的计算思想是计算氨基酸j对应的列中,行为氨基酸i的值求和,因为有20种氨基酸,所以可以将蛋白质序列嵌入成一个400维的向量。
四、smoothed-PSSM
Cheng, C.W., et al. (2008) Predicting RNA-binding sites of proteins using support vector machines and evolutionary information, BMC Bioinformatics, 9 Suppl 12, S6.
设定一个窗口值w,对于原始PSSM中的每一行,向上取w行,向下再取w行,构成一个2w+1行的窗口,在窗口内对每一列求和,将最后的计算结果替代最初选中的行。当超出矩阵的边界时,用全为0的行补齐。

进行完上述操作后,我们再选取一个窗口值W,对于每一行向上取(W-1)/2行,向下取(W-1)/2 行(超出边界的用全为0的行补齐),加上选中行,一起作为选中行对应氨基酸的嵌入,因此每个氨基酸嵌入的维度为Wx20,具体数值由W决定,POSSUM给出的W为50,因此嵌入结果为1000维。在原论文中,smoothed-PSSM是用来为每个氨基酸嵌入的,并非为整个蛋白质序列嵌入。
五、AB-PSSM/RPM-PSSM
Jeong, J.C., Lin, X. and Chen, X.W. (2011) On position-specific scoring matrix for protein function prediction, IEEE/ACM transactions on computational biology and bioinformatics / IEEE, ACM, 8, 308-315.
AB-PSSM 先将原始PSSM按行分成20份,$B=(B_1,B2,...,B{20})$ 每一份称之为一个block,block的行数由序列原始长度决定(尽量做到每份行数相同),列数为20,对每列求平均值,并对B重新展开,则可得到一个400维的向量作为蛋白质序列的嵌入。
RPM-PSSM 也是将原始的PSSM划分成20个block,与AB-PSSM不同的是,在每一个block内只对每列的正值取平均值,因此最后也可以得到一个400维的向量。
六、k-separated-bigram-PSSM
Saini, H., et al.(2016) Protein Fold Recognition Using Genetic Algorithm Optimized Voting Scheme and Profile Bigram.
k-separated-bigram-PSSM是对DPC-PSSM的一个扩展,k-separated-bigram-PSSM是求相邻k行内两个氨基酸的乘积,并求和,具体计算公式为:
$$
T{m,n}(k)=\sum{i=1}^{L-k}p{i,m}p{i+k,n}\\
(1\leq m,n\leq 20)
$$
k-separated-bigram-PSSM最后也可以得到一个400维的向量。
七、tri-gram-PSSM
Paliwal, K.K., et al. (2014) A tri-gram based feature extraction technique using linear probabilities of position specific scoring matrix for protein fold recognition, IEEE transactions on nanobioscience, 13, 44-50.
tri-gram-PSSM 的具体计算公式为:
$$
T{m,n,r}=\sum{i=1}^{L-2}p{i,m}\times p{i+1,n}\times p_{i+2,r}
$$
从公式可知,相当于用一个大小为3的窗口,计算第一行氨基酸m,第二行氨基酸n,第三行氨基酸r的乘积,并求和。可以生成800维向量。
八、EDP-PSSM/EEDP-PPSM
Zhang, L., Zhao, X. and Kong, L. (2014) Predict protein structural class for low-similarity sequences by evolutionary difference information into the general form of Chou's pseudo amino acid composition, Journal of Theoretical Biology, 355, 105-110.
首先我们先计算ED-PSSM矩阵,该矩阵的维数是20x20:
$$
E=(e_1,e2,...,e{20}),ei=(e{1i},e{2i},...,e{20i})
$$
ED-PSSM中的每一个元素为:
$$
e{k,t}=\frac{1}{L-2}\sum{i=2}^{L-1}x{i-1,i+1}\\
x{i-1,i+1}=(Aver_1-Aver_2)^2\\
Aver1=\frac{p{i-1,k}+p_{i,s}}{2}\\
Aver2=\frac{p{i,s}+p_{i+1,t}}{2}
$$
对ED-PSSM每列求平均就可得到一个20维的向量,也就是EDP-PSSM。
EEDP-PSSM 则是在ED-PSSM的基础上,将其展开成一个400维的向量。
MEDP-PSSM 则是将EDP-PSSM和EEDP-PSSM拼接成一个420维的向量。
九、TPC-PSSM/AATP-PSSM
Zhang, S., Ye, F. and Yuan, X. (2012) Using principal component analysis and support vector machine to predict protein structural class for low-similarity sequences via PSSM, Journal of Biomolecular Structure & Dynamics, 29, 634-642.
TPC-PSSM的计算公式为:
$$
y{i,j}=\frac{\sum{k=1}^{L-1}p{k,i}\times p{k+1,j}}{\sum{j=1}^{20}\sum{k=1}^{L-1}p{k+1,j}\times p{k,i}}
$$
其实也是20种氨基酸两两配对计算,可以得到一个400维的向量。
AATP-PSSM 则是TPC-PSSM和AAC-PSSM的一个结合,因此是一个420维的向量。
十、RPSSM
原始的PSSM是Lx20,20表示20种不同的氨基酸,把每列表示成一个长为L的列向量,则原始PSSM可以表示成一个20维的向量:$D=(P_A,P_R,...,P_V)$。做如下运算:
首先根据特定运算将20维的D向量转换成10维,每一维依旧是长为L的列向量,再将这10维向量转换成Lx10的矩阵RD。
接下来有两部分运算,第一步求RD每列的方差:
$$
DS=\frac{1}{L}\sum{i=1}^{L}(p{i,s}-\bar{p{s}})^2\\
\bar{p{s}}=\frac{1}{L}\sum{i=1}^{L}p{i,s}\\
(s=1,2,...,10;i=1,2,3,...,L)
$$
第二步计算公式如下:
$$
D{s,t}=\frac{1}{L-1}\sum{i=1}^{L-1}\frac{(p{i,s}-p_{i+1,t})^2}{2}\\
(s,t=1,2,3,...,10)
$$
第一步可以得到一个10维的向量,第二步可以得到一个10x10的矩阵,将其展开可得到一个100维的向量,将这两部分拼接则可得到一个110维的向量。原论文中对这110个特征值进行了特征筛选,最后用了其中29个作为特征嵌入。
十一、pse-PSSM
Chou, K.C. and Shen, H.B. (2007) MemType-2L: a web server for predicting membrane proteins and their types by incorporating evolution information through Pse-PSSM, Biochemical and Biophysical Research Communications, 360, 339-345.
首先对原始的PSSM每列求平均值,最后得到一个20维的向量。
根据公式:
$$
Gj=\frac{1}{L-lag}\sum{i=1}^{L-lag}(P{i,j}-p{i+lag,j})^2
$$
也就是求第i行j列和第i+lag行j列的差的平方,遍历所有行并求和。可以得到一个20维的向量。
将二者进行拼接,最后可以得到一个40维的向量。POSSUM官方给出的默认参数是lag=1,也可以用户自己设置。
十二、DP-PSSM
Juan, E.Y., et al. (2009) Predicting Protein Subcellular Localizations for Gram-Negative Bacteria using DP-PSSM and Support Vector Machines. Complex, Intelligent and Software Intensive Systems, 2009. CISIS'09. International Conference on. IEEE, pp. 836-841.
DP-PSSM的计算有点繁琐,公式可能有点多,但是也不难理解。首先明白,DP-PSSM是两部分组成T'和G’,我们先来看看T‘:
$$
T'=[\bar{T}_{1}^P,\bar{T}_1^N,\bar{T}_2^P,\bar{T}_2^N,...,\bar{T}_{20}^P,\bar{T}_{20}^N]
$$
$NP_j,NN_j$表示矩阵T的第j列中正数(包括0)和复数的数量,上述公式表示分别对矩阵T的第j列中的正数和负数求平均值,可以得到一个40维的向量。
矩阵T是由原始PSSM计算得到的,具体计算公式为:
其实就是对原始PSSM做行归一化,计算每行的平均值和标准差,再让对应行的所有元素减去均值并除以标准差,因此矩阵T和PSSM的形状一致。
G’:
可以看出G‘实际上是一个二维矩阵,其中每项的计算公式为:
公式的基本原理是,计算矩阵T的第i行和第i+k行中第j列的差的平方,根据二者的大小计算的公式略有不同,其实和T’计算规则大致相似。将G‘展开即可得到一个40α的向量。
将两者进行拼接,最后可以得到一个40+40α的向量,原论文中给出的α的值为2,最后可以将蛋白质嵌入成一个120维的向量。但是POSSUM上给出的默认值是5,最后给出的结果则是240维向量。
十三、PSSM-AC/PSSM-CC
Dong, Q., Zhou, S. and Guan, J. (2009) A new taxonomy-based protein fold recognition approach based on autocross-covariance transformation, Bioinformatics, 25, 2655-2662.
PSSM-AC 的计算公式为:
$$
AC(lg,j)=\frac{1}{L-lg}\sum{i=1}^{L-lg}(s{i,j}-\bar{sj})(s{i+1,j}-\bar{s_j})\\
\bar{sj}=\frac{1}{L}\sum{i=1}^{L}s_{i,j}
$$
PSSM-AC是一个LGx20维的向量,LG表示lg的最大值,POSSUM给出的LG为10。
PSSM-CC 的计算公式为:
$$
CC(j1,j2,lg)=\frac{1}{L-lg}\sum{i=1}^{L-lg}(s{i,j1}-\bar{s{j1}})(s{i+lg,j2}-\bar{s_{j2}})
$$
会产生20x19xLG维向量。
十四、小结
上述内容其实还缺少一种PSSM,PSSM-composition,我还没有弄清其具体原理,大致计算方法是统计每行氨基酸为i的第j列分值,最后会得到一个400维的向量。
上述内容参考:
PSSMCOOL还给出了POSSUM没有的PSSM,感兴趣的可以看看。

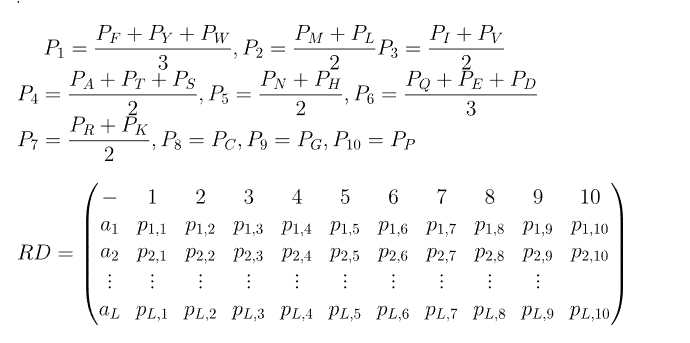
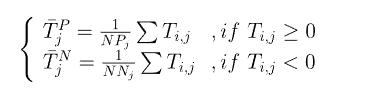
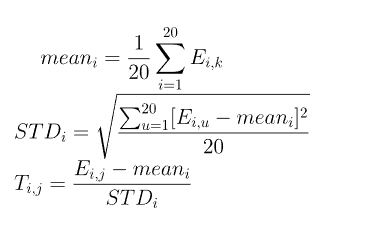
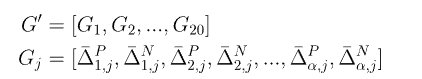
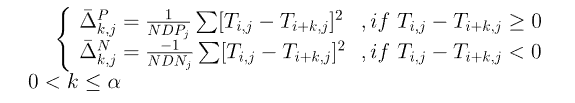

Great site, amazing style and design, very clean and user-friendly. Gladi Weber Amatruda.
I really enjoyed reading this post, thank you! Fantastic job!
Hi! I read through this post and it reminds me of my old roommate who would always talk about similar topics. I will definitely forward this to him. Thank you for sharing!
I would like to know where you got your website theme or design. Could you please share that information with me?
I would like to know where you got your website theme or design. Could you please share that information with me?
Hi there, are you genuinely visiting this site on a regular basis? If so, then you will definitely gain fastidious knowledge.
I would like to know where you got your website theme or design. Could you please share that information with me?
很感兴趣,但是特征的计算公式似乎没有正确显示